Spring is only days away. Let’s clean out the cobwebs and solve the Sudoku challenges this month!
Clueless?
We start with a Sudoku puzzle in progress, where it appears that there are no more obvious or not-so-obvious clues. Can you find the hidden clue in Puzzle #141?

(The answer follows the conclusion of Puzzle #144, the feature puzzle for this month)
Just Logic Puzzle
Difficult rating … 7/10
(Rating based on puzzles not requiring advanced techniques)

Hint … be relentless searching for clues.
Impossible to solve?
Impossible? No. Difficult? Extremely.
Puzzle #143 should be quite a challenge. Advanced Techniques (Steps 6 and/or 7) are required. Difficult rating 9.5/10.
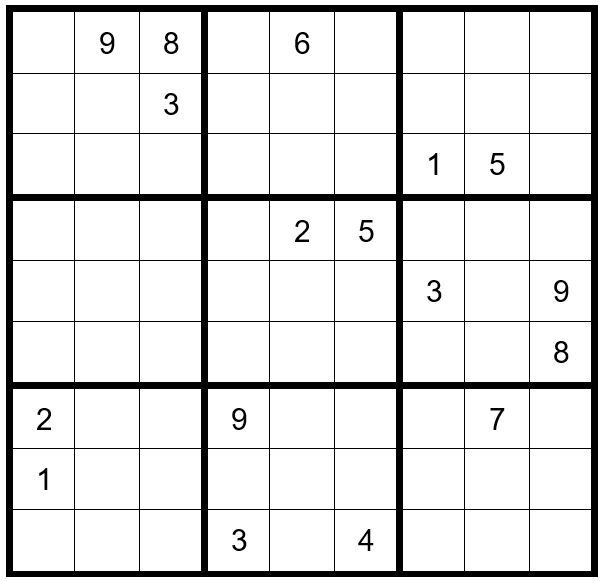
Feature Puzzle
Difficult rating … 3/10
(Rating based on puzzles requiring advanced techniques)

PUZZLE PREPARATION
Prior to utilizing techniques 1-8, complete the 5 Steps of Puzzle Preparation …
- FILL IN DATA FROM OBSERVATIONS
- FILL IN OBVIOUS ANSWERS
- FILL IN NOT-SO-OBVIOUS ANSWERS
- MARK UNSOLVED CELLS WITH OPTIONS THAT CANNOT EXIST IN THOSE CELLS
- FILL IN THE OPTIONS FOR THE UNSOLVED CELLS
The first thing we observe is that C1R4=1. C5R9=1.
C7R1 & C7R3 have options 5 & 8.
In box four a 5 can only exist as an option in C2R4 and C2R5; therefore, a 5 cannot exist as an op-tion in C2R1, C2R3, C2R8 and C2R9.
In row six C1R6, C2R6, C3R6 & C6R6 are limited to options 2, 4, 7 & 8. Then, C5R6, C7R6 & C9R6 are limited to options 3, 6 & 9. Since a 3 and 9 already exist in column 9, C9R6=6.
Ok, let’s pause here to explain a technique used to identify situations like this that frequently appear. If you look at row six, you know that one of the given answers (1) matches the 1 in box four. Look for a column associated with row 6 that might have three of the other given numbers in box four. Yes, in this case there is a 3, 6 & 9 in column six. Bingo, we have detected a quad in row six, and in this case, we know we have a triplet in row six as well. Ponder on this and work it out in your mind how to easily recognize these situations.
C5R6 & C7R6 have options 3 & 9.
In box eight a 5 can only exist as an option in C5R7 and C6R7; therefore, a 5 cannot exist as an option in C1R7, C3R7 & C9R7.
Now your grid should look like Example #144.1 below:

Please note: options for C6R6 are limited to 2 & 4. The 7 is eliminated as an option by C6R4. The 8 is limited by C1R6 & C3R6 being the only two cells in box four that can be an 8.
This completes Puzzle Preparation Steps 1-4.
Normally, next we would fill in options for all of the unsolved cells. However, there are two options that would make excellent candidates for Step 6 exercises.
As in previous articles, we determined a particular number was a potential for a successful Step 6 exercise if that number appears as a given answer in 3 separate boxes, such that the boxes are not side-by-side, nor over each other. Which numbers do you see that are good candidates? Yes, the 3’s & 9’s. We do not need the options of the unsolved cells to be listed in order to con-duct these exercises. If one or both of these exercises is successful, we could save quite a bit of time not having to fill in the options for all unsolved cells and potentially shortening the time to solve the puzzle.
We will start with the 3’s and perform a Step 6 exercise, Dan’s Yes-No Challenge”, per Example #144.2 below, using C1R2 & C5R2 as our starter cells highlighted in yellow.

Either C1R2 or C5R2 has to be a 3. First, we will assume C1R2=3 and mark it with a capital Y, for yes. Then we will mark the cells it affects in other boxes with a Y or N, indicating a yes or no.
Next, we will assume C5R2=5, and mark it with a “y”. Then we will mark the cells it affects with a y or n.

We see that C1R7, C7R8 & C8R5 are marked N,n. It means that these cells cannot be a 3, regardless of which starter cell is a 3. The 3 can be eliminated as an option for those cells. We also see that C8R7 is marked with a Y,y, meaning that cell is a 3 regardless of which starting cell is a 3; therefore, C8R7=3.
Now our grid should look like Example #144.4 below:

We can now see that a 9 can only exist as an option in box 9 in C7R9 and C8R9; therefore a 9 cannot exist as an option in C2R9 & C3R9. Thus, C3R7=9. C2R1=9.
C5R2=9 and so forth. It is downhill from here, leading us to an easy conclusion, as per Example # 144.5 below.

May the gentle winds of Sudoku be at your back.
By Dan LeKander
Clue for Puzzle #141 … did you find the clue? If not, read on.
Check column 9. What do you see?
We see that C9R3, C9R5 & C9R6 are the only three cells in row 3 that can have options 4, 5 & 8. Since there already exists a 4 & 8 in row 6, C9R6=5.
Important Editor's Note
We need to hear from you - do you work on Dan's Sudoku's Puzzles
Dan would like to hear more from his readers, such as questions, comments & suggestions. To confidentially reach Dan please e-mail him to this link - info@thousandislandslife.com. We will forward this to Dan, and he will contact you directly. Thank you."
Recently someone wrote to ask how to fill them out online. Unfortunately, you need to print them yourself, but that is easy to do and I know you will have just as much fun. Also you can use a grid sheet and copy numbers onto the grid.
And, if you have not already done so, I suggest you purchase Dan’s book: