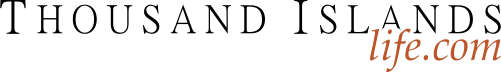We continue with 3 puzzles each month. See if you can solve all 3!
Clueless?
We start with a Sudoku puzzle in progress, where it appears there are no more obvious or not-so-obvious clues. Can you find the hidden clue in Puzzle #113?
PUZZLE #113
(The answer follows the conclusion of Puzzle #115, the feature puzzle for June)
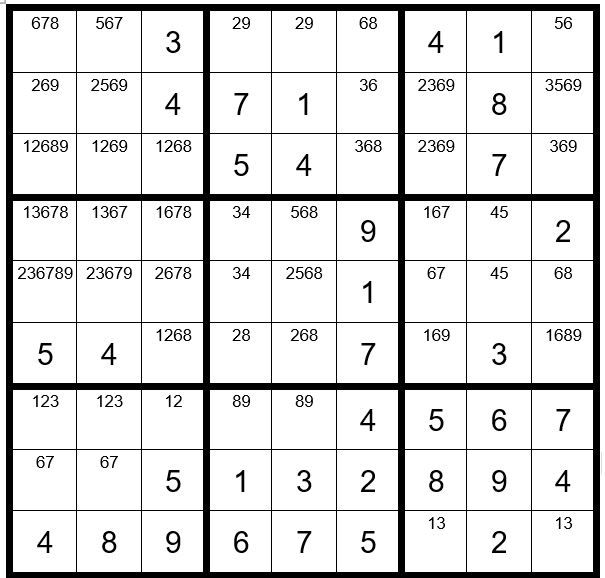
Logic Puzzle: Difficult rating … 8/10
(Rating based on puzzles not requiring advanced techniques)
Puzzle # 114
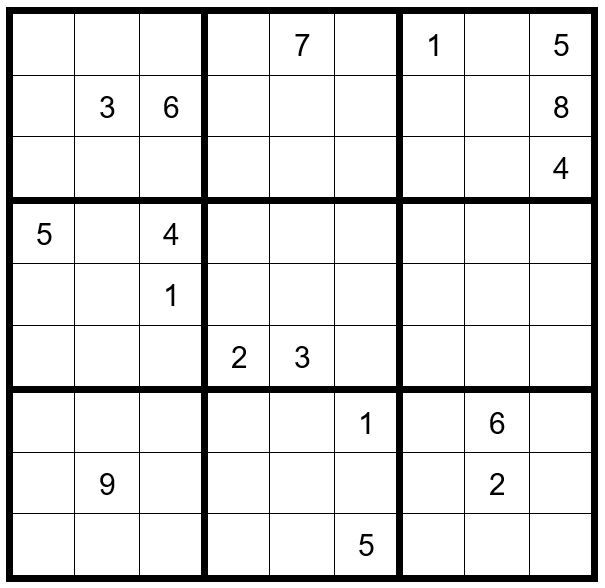
Puzzle #114 should provide a good challenge.
Puzzle #115
Feature Puzzle: Difficult rating … 6/10
(Rating based on puzzles requiring advanced techniques)
Print this puzzle and give it a go.
Dan recommends the following Steps to complete the puzzle.
Step 1: Sudoku Pairs, Triplets and Quads – See September 2015
Step 2: Turbos & Interaction – See October 2015
Step 3: Sudoku Gordonian Rectangles and Polygons – See November 2015
Step 4: XY-Wings & XYZ Wings – See December 2015
Step 5: X-Wings – See January 2016
Step 6: DAN’S YES/NO CHALLENGE
Step 7: DAN’S CLOSE RELATIONSHIP CHALLENGE
Step 8: AN EXPANSION OF STEP 7Steps 1-5 are relatively common techniques and are explained in the TI LIFE articles above. Steps 6-8 are covered in detail, in Dan’s book.

PUZZLE PREPARATION
Prior to utilizing Steps 1-8, complete the 5 Steps of Puzzle Preparation …
- FILL IN DATA FROM OBSERVATIONS
- FILL IN OBVIOUS ANSWERS
- FILL IN NOT-SO-OBVIOUS ANSWERS
- MARK UNSOLVED CELLS WITH OPTIONS THAT CANNOT EXIST IN THOSE CELLS
- FILL IN THE OPTIONS FOR THE UNSOLVED CELLS
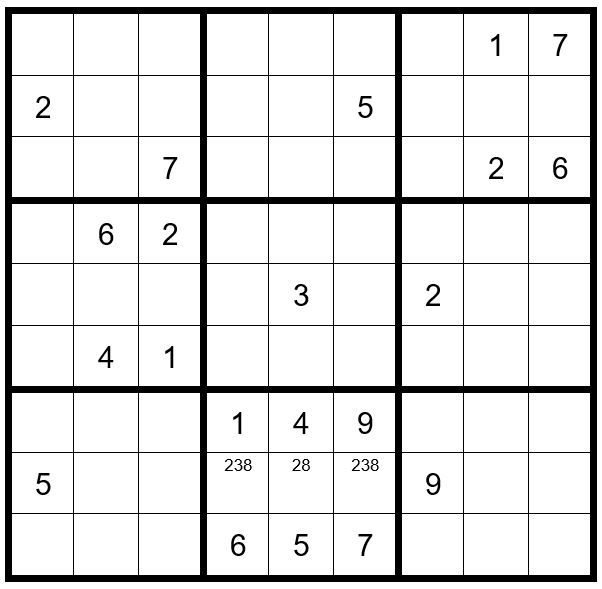
We observe the following clues ... C8R2=2, C3R4=2, C5R9=5 & C6R7=9.
C4R8, C5R8 & C6R8 have option possibilities of 2, 3 & 8
Now your grid should like Example #115.1 below:
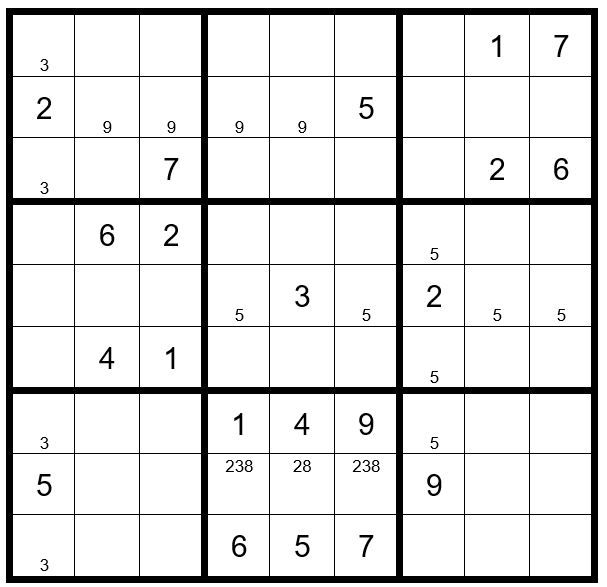
In box 4 a 3 can only exist as an option in C1R4 & C1R6; therefore, a 3 cannot exist as an option in in C1R1, C1R3, C1R7 & C1R9.
In box 3 a 5 can only exist as an option in C7R1 or C7R3; therefore, a 5 cannot exist as an option in C7R4, C7R6 & C7R7.
In box 4 a 5 can only exist as an option in C2R5 & C3R5; therefore, a 5 cannot exist as an option in C4R5, C6R5, C8R5 & C9R5.
In box 3 a 9 can only exist as an option in C8R2 & C9R2; therefore, a 9 cannot exist as an option in in C2R2, C3R2, C4R2 & C5R2.
Now your grid looks like Example #115.2 Below:
This completes Puzzle Preparation Steps 1-4, but before we will fill in the options for all unsolved cells, we will do a quick check for potential Step 6 exercises.
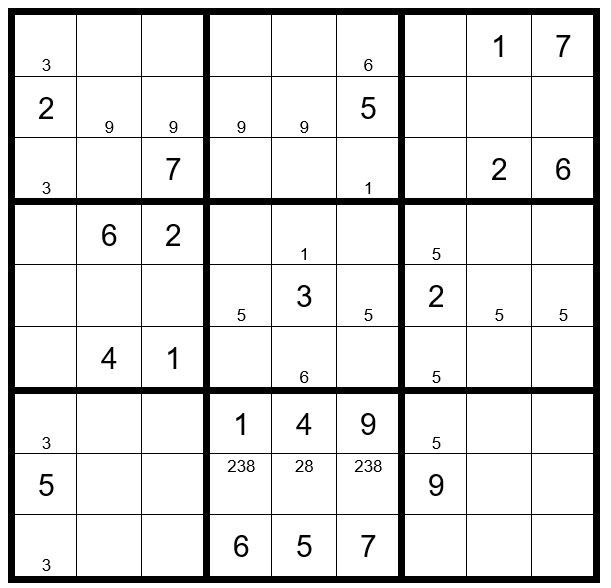
As in previous articles, we determined a particular number was a potential for a successful Step 6 exercise if that number appears as a given answer in 3 separate boxes, such that the boxes are not side-by-side, nor over each other. Which numbers do you see that are good candidates? Yes, 1 and 6.
By completing the Step 6 exercise for the 1’s, you find that C5R4 & C6R3 cannot be a 1 regard-less of which two starter cells you use.
By completing the Step 6 exercise for the 6’s, you find that C6R1 & C5R6 cannot be a 6.
These clues do not give us further clues.
Now your grid should look like Example #115.3 below:
Next, we fill in the options for the unsolved cell, giving up Example #115.4 below:
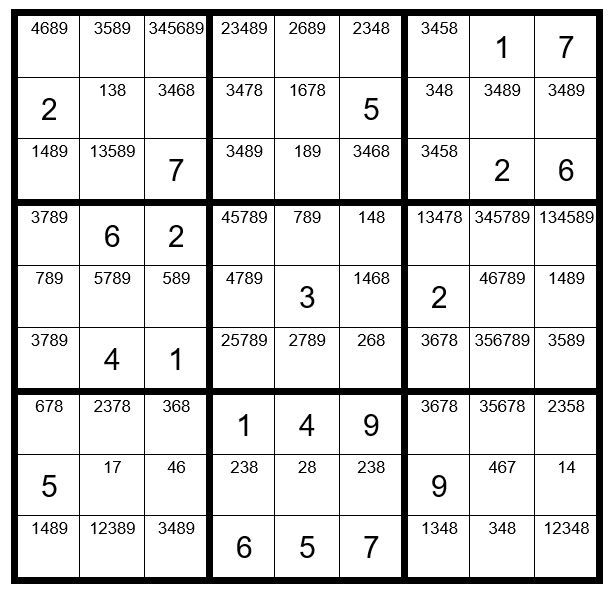
There are no Step 1-5 clues, so we will proceed to Step 7, Dan’s Close Relationship Challenge.
We will pick C3R8 as our starter cell, with a sequence of 6,4. We will annotate this on the 2nd level of this cell, as per Example #115.4 below.
So, why did I pick as a starter cell C3R8 with a sequence 6,4? Quite simply I realized that if C3R8=4, we would have immediate answers for C2R8, C8R8 and C9R8. This almost guarantees that the 4 would track through the puzzle far enough to give us positive results.
Please refer to Example #115.5 below:
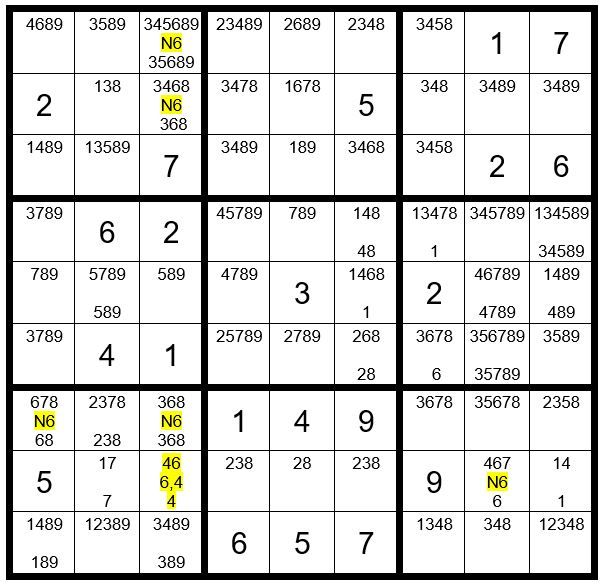
We begin by asking ourselves that if this starter cell is a 6, what adjacent cells could not be a 6, annotating and yellow highlighting those cells as “N6”, again on the 2nd level of those cells. This just simply means that if the starter cell is a 6, then those cells cannot be a 6.
Next, we assume the starter cell is a 4 and track the results through the puzzle. If any N6 cell is a number other than 6, it means that cell is not a 6 regardless if the starter cell is a 6 or 4, and the 6 could be eliminated as an option from that cell.
Before we perform this exercise, we will list the potential outcomes …
• The tracking of the second number of the starter cell doesn’t reach the N9 cells, and there-fore, the exercise is unsuccessful.
• The tracking of the second number goes entirely through the puzzle without a conflict, indicating that the 2nd number is correct for the starter cell and you have solved the puzzle.
• The tracking of the second number creates a conflict, such as a number showing up twice in a row, column or box. Or it could show up by having no cell for a particular number in a row, column or box. Regardless of how the conflict arises, it would mean the second number is incorrect for that cell, and therefore, the answer to the starter cell is the first number.
We will now track the 4 through the puzzle above on the third level of the unsolved cells to pre-serve the integrity of the original puzzle.
As you can see from the example above, in tracking the 4 through the puzzle, there is not an un-solved cell in box 5 that can be a 6. This is a conflict! Therefore, C3R8=6.
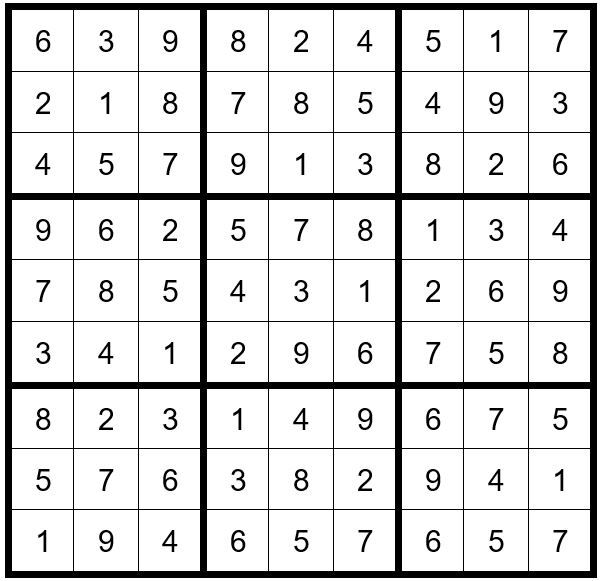
The puzzle is easily solved from this point and the solution is Example #115.6 below:
May the gentle winds of Sudoku be at your back.
Dan LeKander
Clue for Puzzle #113 … did you find the clue? If not, read on.
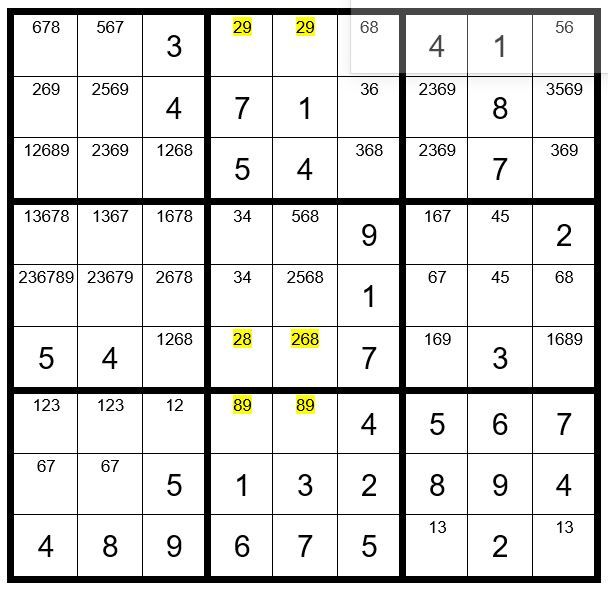
Check out the six unsolved cells highlighted in yellow. This is a classic Gordonian polygon. C5R6 cannot have options 28, as this would create a puzzle with multiple answers. Therefore, C5R6=6.
When I finished solving this puzzle, I still had to use advanced technique, Step 7. Clue … find the right starter cell with the correct sequence.
Editor's Note: Note: we went into the 100s in May 2022
Now here are Puzzles #113, #114, and #115.
"I keep saying . . . when we published the final article in Dan's Series of steps to learn the logic of Sudoku, I never in a zillion years thought that Dan would so graciously offer to do one or two puzzles for us each month - and he has done so without my asking. Now we are up to 3!
Then his wife, Peggy, does the proof reading and I only have to post in on TI Life. We would love to know how many you have solved. (Many, darn it, have stumped me, but I look forward to them each month.)
In May someone wrote to ask how to fill them out online. Unfortunately, you need to print them yourself - but that is easy to do and I know you will have just as much fun.
And, if you have not already done so, I suggest you purchase Dan’s book: