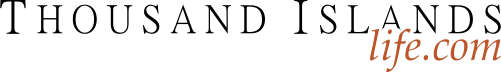August is in full swing. What a great time to tackle another “impossible” puzzle.
Print out the grid and give it a go, or follow my lead.
DAN’S 8-STEP APPROACH TO SOLVING ALL SUDOKU PUZZLES
Once you have completed the puzzle, to the extent that you have filled-in all obvious answers and have written all potential options across the top of the unsolved cells (PUZZLE PREPARATION), Dan recommends the following Steps to complete the puzzle.
Step 1: Sudoku Pairs, Triplets and Quads – See September 2015
Step 2: Turbos & Interaction – See October 2015
Step 3: Sudoku Gordonian Rectangles and Polygons – See November 2015
Step 4: XY-Wings & XYZ Wings – See December 2015
Step 5: X-Wings – See January 2016
Step 6: DAN’S YES/NO CHALLENGE
Step 7: DAN’S CLOSE RELATIONSHIP CHALLENGE
Step 8: AN EXPANSION OF STEP 7Steps 1-5 are relatively common techniques and are explained in the TI LIFE articles above. Steps 6-8 are covered in detail, in Dan’s book.

PUZZLE PREPARATION
Prior to utilizing techniques first complete the 5 Steps of Puzzle Preparation …
- FILL IN DATA FROM OBSERVATIONS
- FILL IN OBVIOUS ANSWERS
- FILL IN NOT-SO-OBVIOUS ANSWERS
- MARK UNSOLVED CELLS WITH OPTIONS THAT CANNOT EXIST IN THOSE CELLS
- FILL IN THE OPTIONS FOR THE UNSOLVED CELLS
We will complete all of the first 4 steps in the order we observe them.
We will start with the 1’s and navigate through 2’s to 9’s, then repeat the process until we conclude all Puzzle Preparation Step 1-4 clues.
The first thing we observe is that C1R3 (cell in column 1, row 3) =1 (obvious answer). Then, C3R1=5. C6R4=9. C8R8=9.
In box 9 a 1 can only exist in C9R7 or C9R8; therefore, a 1 cannot exist as an option in C9R2, C9R4 or C9R6. Indicate this by placing a small 1 in the bottom of those cells.
In box 5 a 1 can only exist in C4R5 or C6R5; therefore, a 1 cannot exist as an option in C3R5, C7R5 or C8R5.
In box 9 a 2 can only exist in C7R9 or C8R9; therefore, a 2 cannot exist as an option in C1R9, C3R9, C4R9 or C6R9.
In box 5 a 5 can only exist in C5R4 or C5R6; therefore, a 5 cannot exist as an option in C5R2, C5R3, C5R7 or C5R8.
Now your grid should look like Example #68.1 below:
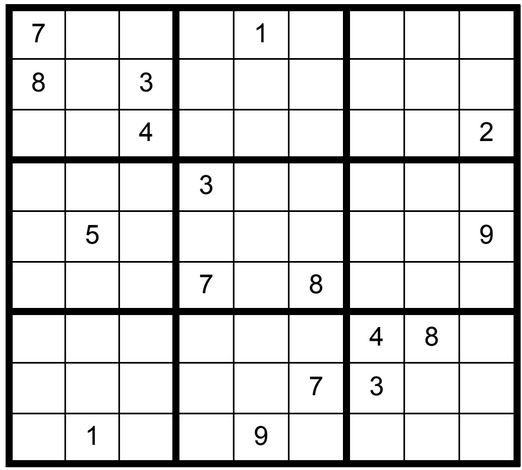
This concludes Puzzle Preparation steps 1-4. We will now fill in the options for the unsolved cells. Remember, there is an obvious triplet in C2R1, C2R2 & C2R3. Now your grid should look like Example #68.2 below:
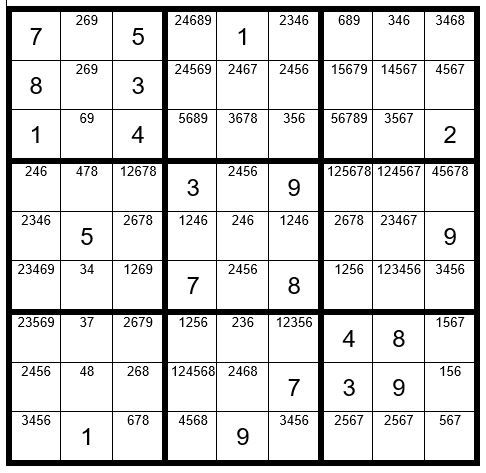
STEPS 1-5
There are no Step 1-5 clues, so we will now proceed to Step 6: Dan’s Yes-No Challenge.
There are 3 circumstances that establish the potential for a Step 6 exercise:
- Look for just 2 unsolved cells in a box that contain the same option where these 2 cells are not in the same row or column.
- Look for just 2 unsolved cells in a column that contain the same option where these 2 cells are not in the same box.
- Look for just 2 unsolved cells in a row that contain the same option where these 2 cells are not in the same box.
We will start by searching the 1’s to see if there is a potential Step 6 clue, and then navigate through the 2-9’s.

In the example above we find two unsolved cells in column 2 that have the option 3 (C2R6 & C2R7), and are not in the same box, thereby qualifying for a Step 6 exercise. We will call these two cells our “driver cells” which drive the exercise. One of these two cells must be a 3. We will first start with C2R6 and assume it is the 3, to see what effect it has on the other unsolved cells with option 3. Then, we will assume C2R7 is the 3, to see what effect it has on the other unsolved cells. We will annotate C2R6 with a “Y” for yes, and annotate C2R7 with “y” to indicate yes.
If C2R6 is the 3, then C8R6 & C9R6 are not a 3, indicated by N. Then C8R5=Y, C8R1=N & C8R3=N. C9R1=Y. C6R1=N.
If C2R7 is the 3, then C5R7=n & C6R7=n. C6R9=y. C6R1 & C6R3=n, C5R3=y.
C8R3=n.You can see that two cells, C6R1 & C8R3 have N,n designations. This means regardless of which of the two driver cells in column 2 is a 3, these cells cannot be a 3. You may eliminate the 3 as an option from these two unsolved cells, giving us Example #68.4 below:
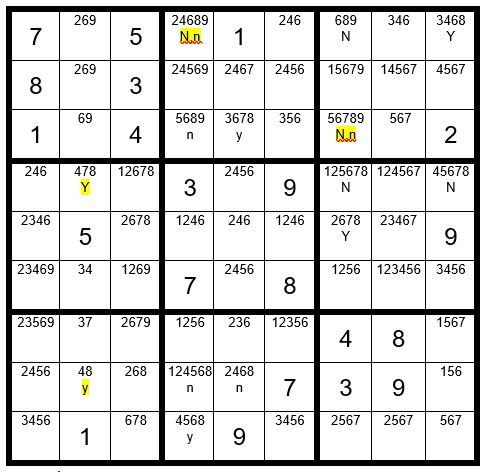
In Example #68.4 above we also find two cells in column 2 that contain the option 8, and are not in the same box. These will be our driver cells for this exercise. Assign the values to the other unsolved cells that have the 8 as an option. Again we generate two cells with the N,n designation. You may remove the option 8 from those two cells, giving us Example #68.5 below:
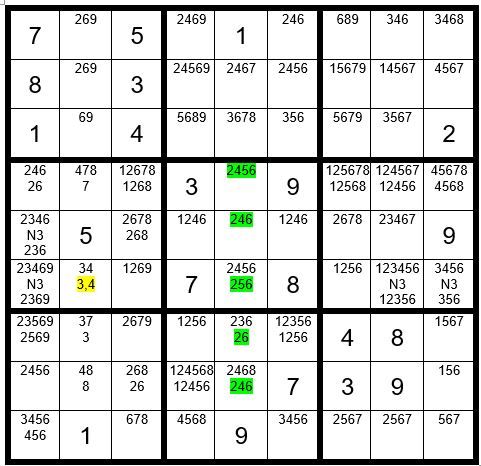
There are no other Step 6 exercises with productive results, so we will move on to Step 7.
Step 7: Dan’s Close Relationship Challenge. In this exercise we will select any two-option unsolved cell as the driver cell. My first choice is C2R6 with the sequence 3,4 as marked above in Example #68.5. I chose this cell and sequence because the cell has adjacent unsolved cells with 3 as an option and the 4 may track through the puzzle to give us significant information.
We know that C2R6 must be a 3 or 4. First, we will assume it is a 3. If this is true, then C1R5, C1R6, C8R6 & C9R6 cannot be a 3 (hence the notation N3).
Next, we will assume C2R6 is a 4. We will track the 4 through the grid on the next lower level to see the value of unsolved cells. Tracking in this fashion preserves the original puzzle on the top level of each cell. If an N3 cell is a value other than 3, then we know that it is not a 3 regardless of whether C2R6 is a 3 or 4.
We track C2R6 being a 4 through the grid above in the lower level of each unsolved cell in Example #68.5 above. C2R8=8. C2R4=7. C2R7=3.
We will pause here and look at column 5. What do you see? The 5 cells marked in green want to share only 4 options, 2456. That would not work well.
We see that this is a conflict. It is not as obvious as, say, two 4’s in a column, but it is a valid conflict. What does this mean? It mean that C2R6 cannot be a 4; therefore, C2R6=3, giving us Example #68.6 below:
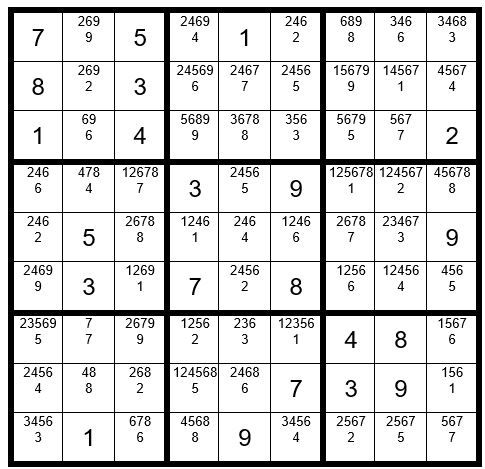
Track the 3 in C2R6 and it follows that C2R7=7. C8R5=3. C9R1=3. Now the only cell in box 3 that can be an 8 is C7R1. C7R1=8. C9R4=8. C2R4=4. C2R8=8. C3R9=6. C4R9=8. C5R3=8, and so forth, leading to a conclusion for the puzzle.
Saved by Step 7 to see another day!
May the gentle winds of Sudoku be at your back.
Dan LeKander