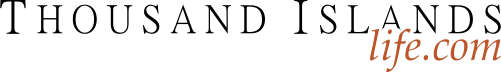Sudoku Puzzle #49

This month we will take Puzzle Preparation to the next level!

DAN’S 8-STEP APPROACH TO SOLVING ALL SUDOKU PUZZLES

Once you have completed the puzzle, to the extent that you have filled-in all obvious answers and have written all potential options across the top of the unsolved cells (PUZZLE PREPARATION), Dan recommends the following Steps to complete the puzzle.

Step 1:  Sudoku Pairs, Triplets and Quads – September 2015

Step 2:  Turbos & Interaction – October 2015

Step 3:  Sudoku Gordonian Rectangles and Polygons – November 2015

Step 4:  XY-Wings & XYZ Wings – December 2015

Step 5:  X-Wings – January 2016

________________

Step 6:  DAN’S YES/NO CHALLENGE

Step 7:  DAN’S CLOSE RELATIONSHIP CHALLENGE

Step 8:  AN EXPANSION OF STEP 7

Steps 1-5 are relatively common techniques and are explained in the TI LIFE articles above. Steps 6-8 are covered in detail, in Dan’s book.

Also, see Sudoku Puzzle Challenge… February 2016, March 2016, April 2016, May 2016, June 2016, July 2016, August 2016, September 2016, October 2016, November 2016,  December 2016, January 2017, February 2017, March 2017 , April 2017,  May 2017, June 2017, July 2017, August 2017, September 2017, October 2017 , November 2017 ,  December 2017, January 2018, February 2018, March 2018, April 2018. May 2018, June 2018, July 2018, August 2018, September 2018 , October 2018, November 2018, December 2018 and January 2019.

As a reminder, the basic rules of Sudoku are that the numbers 1-9 must be contained and cannot be repeated in a row, column, or box, and there can only be one solution to the puzzle.

PUZZLE PREPARATION

Prior to utilizing techniques first complete the 4 Steps of Puzzle Preparation …

1. FILL IN OBVIOUS ANSWERS
2. FILL IN NOT-SO-OBVIOUS ANSWERS
3. MARK UNSOLVED CELLS      WITH OPTIONS THAT CANNOT EXIST IN THOSE CELLS
4. FILL IN THE OPTIONS FOR      THE UNSOLVED CELLS

OBVIOUS ANSWERS …

Start with the 1’s to see if there are any obvious 1-choice answers. Then navigate the 2’s through 9’s.

The first obvious answer is C5R3 (cell in column 5, row 3) = 6.  C3R4=8.  Now your grid should look like Example 49.1 below:

NOT-SO-OBVIOUS ANSWERS … there are none.

MARK UNSOLVED CELLS WITH OPTIONS THAT CANNOT EXIST IN THOSE CELLS …

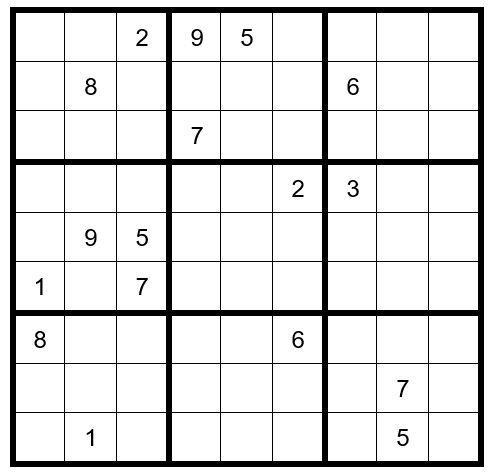
In box 2 (upper center box of 3 x 3 cells) C4R2 & C5R2 are the only two cells that can have the option 2; therefore, a 2 cannot exist in C8R2 or C9R2.   Pencil a small 2 in the bottom of those two cells to indicate they cannot be a 2.  This will be handy when you fill in options for the unsolved cells.

In looking at the 2’s, we notice that C1R4 & C2R4 cannot be a 2 or 3; therefore, C1R5 & C2R6 must have options 23.  This leaves us with options 4 & 6 as the only two options for C1R4 & C2R4.  So, we will pencil in the options for the unsolved cells in box 4.

In box 2 C6R1 & C6R3 are the only two cells that can have the option 8; therefore, an 8 cannot exist in C6R5, C6R6, C6R8 or C6R9.  

Now we will examine the grid a bit further.   We will start by looking at column 8.  The only cells that can have a 6 as an option are C8R5 & C8R6; therefore, a 6 cannot exist in C9R5 & C9R6.  (We already know a 6 cannot exist in C8R4 or C9R4 because of the pair 46 in C1R4 & C2R4).

Next, we will examine column 3.  A 6 can only exist in cells C3R8 & C3R9; therefore, a 6 cannot exist in C1R8, C1R9 & C2R8.

You might ask, what happens if you miss the clues in the last two paragraphs.  They would appear in Steps 1-5 as Interactions, and would produce the same grid.  

Now your grid should look like Example #49.2 below:

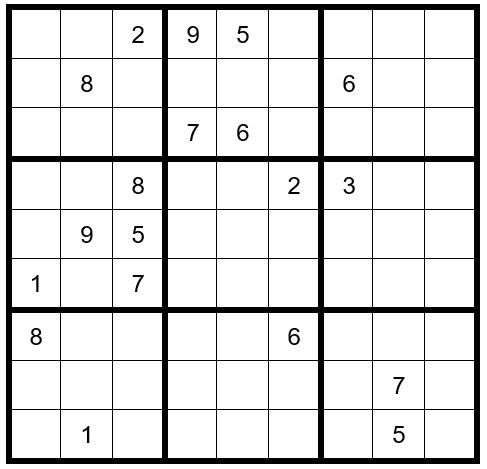
FILL IN THE OPTIONS FOR THE UNSOLVED CELLS …

Once you fill in the options for the unsolved cells, your grid should look like Example #49.3 below:

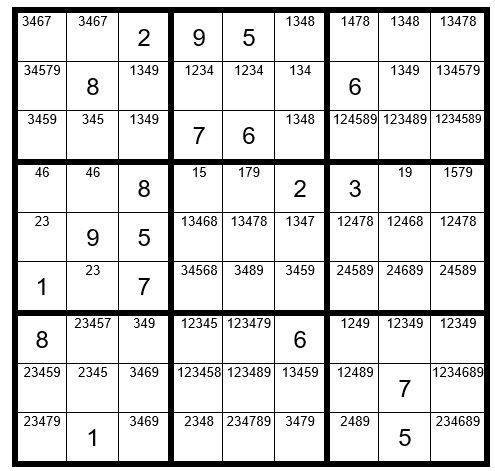
STEPS 1-8

We search all rows, columns & boxes in Step 1 for Pairs, Triplets & Quads.   In row two only 2 unsolved cells contain the 2 options 5 & 7, a hidden pair.  We change the options for those cells to 57.  Now your grid should look like Example # 49.4 below:

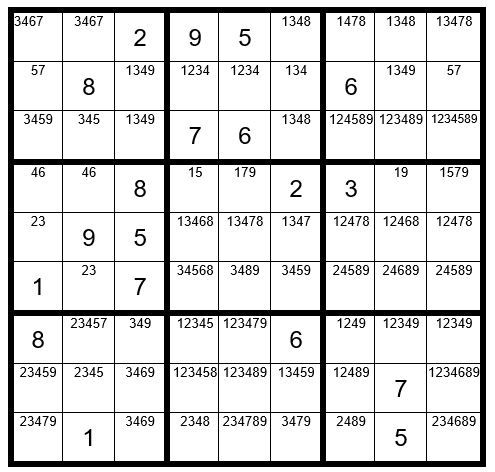
There are no additional Step 1-5 clues.

We will now move to Step 6:  Dan’s Yes-No Challenge.

There are 3 circumstances that establish the potential for a Step 6 exercise:

1. Look for just 2 unsolved cells in a box      that contain the same option where these 2 cells are not in the      same row or column.
2. Look for just 2 unsolved cells in a column      that contain the same option where these 2 cells are not in the      same box.
3. Look for just 2 unsolved cells in a row      that contain the same option where these 2 cells are not in the      same box.

We will start by searching the 1’s to see if there is a potential Step 6 clue, and then navigate through the 2-9’s.

In column 6 we find just 2 unsolved cells that contain the option 5 … C6R6 & C6R8.  These cells are not in the same box, thereby qualifying as a candidate for a Step 6 exercise.  The options in these cells are highlighted in yellow in Example #49.5 below:

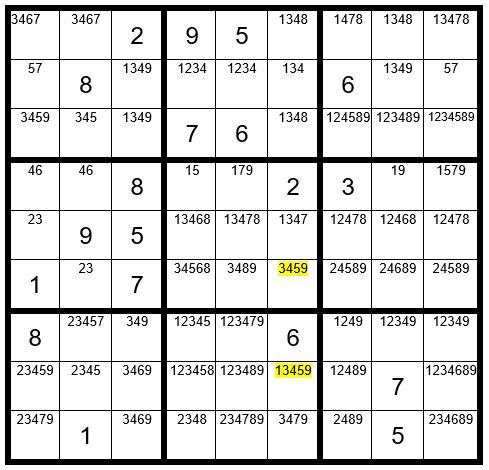
Do you agree that one of these two yellow cells in column 6 must be a 5?   We will consider them as “driver cells” which “drive” the exercise.

Here is the logic.  We will perform two exercises.  First, we will assume C6R6 is the 5 and see which other cells cannot be a 5.  Then we will assume C6R8 is the 5 and see which other cells cannot be a 5.  

We will mark C6R6 with a “Y” and mark C6R8 with a lower case “y” to keep track of the exercise as per Example #49.6 below.  

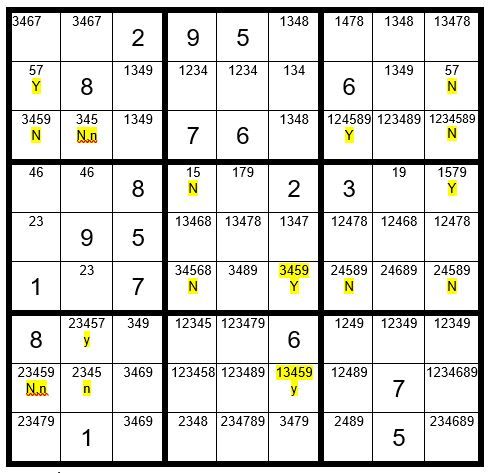
We will start by assuming C6R6=5.  Then, as marked above, C4R4, C4R6, C7R6 & C9R6 are not a 5 (marked with a “N”).  Now the only cell in box 6 that can be a 5 is C9R4, so we will mark it as a “Y”.  Then, C9R2=N.  C9R3=N.  C7R3=Y.  C1R3=N.  C2R3=N.  C1R2=Y.  C1R8=N.  

Now we will assume C6R8=3 (y for yes).  Then, C1R8=n.  C2R8=n.  C2R7=y.  C2R3=n.

We now see in Example #49.6 above that C1R8 & C2R3 have a “N,n” designation.  What does that mean?  Since we know one of the two yellow highlighted cells in column 6 must be a 5, the N,ncells cannot be a 5 regardless of which starter cell is a 5.  We eliminate the 5 as an option from C1R8 & C2R3.

Now your grid should look like Example #49.7 below:

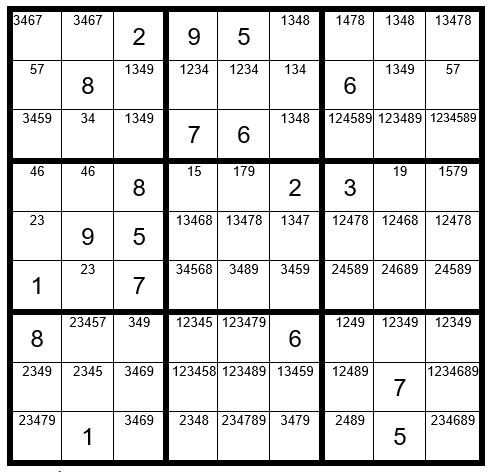
We now need another clue, so we will look for another Step 6 exercise.

In column 2 we find just 2 unsolved cells that contain the option 7 … C2R1 & C2R7.  These cells are not in the same box, thereby qualifying as a candidate for a Step 6 exercise.  The options in these cells are highlighted in yellow in Example #49.8 below:

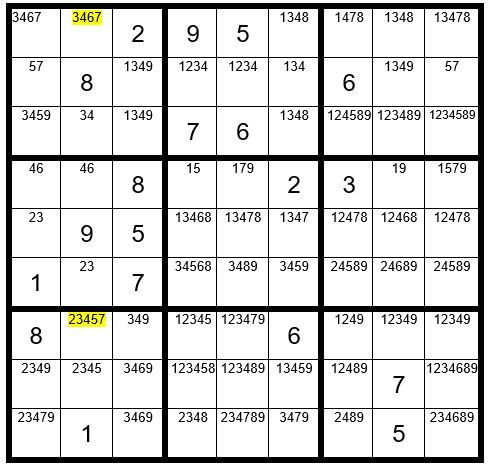
We will mark C2R1 with a “Y” and mark C2R7 with a lower case “y” to keep track of the exercise as per Example #49.9 below.

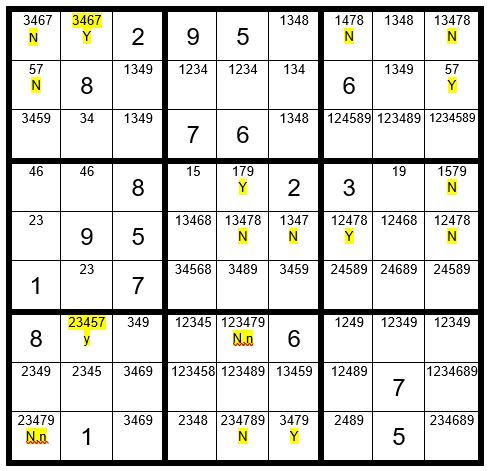
We will start by assuming C2R1=7.  Then, as marked above, C7R1, C9R1, C1R1 & C1R2 are not a 7 (marked with a “N”).  Now the only cell in box 3 that can be a 7 is C9R2, so we will mark it as a “Y”.  Then, C9R4=N.  C9R5=N.  C7R5=Y.  C5R5=N.  C6R5=N.  C5R4=Y.  C5R7=N.  C5R9=N.  C6R9=Y.  C1R9=N.

Now we will assume C2R7=7 (y for yes).  Then, C1R9=n.  C5R7=n.  

We now see in Example #49.9 above that C1R9 & C5R7 have a “N,n” designation.  The N,n cells cannot be a 7 regardless of which starter cell is a 7.  We eliminate the 7 as an option from C1R9 & C5R7.

Now your grid should look like Example #49.10 below:

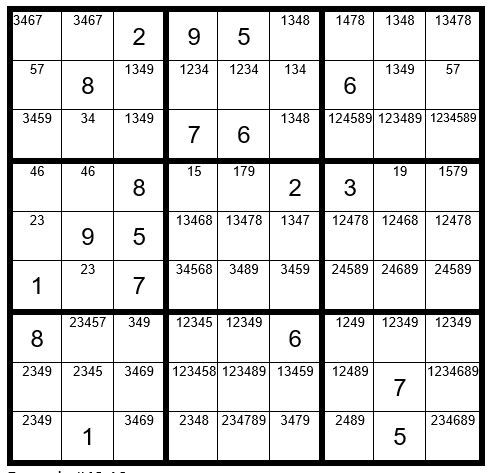
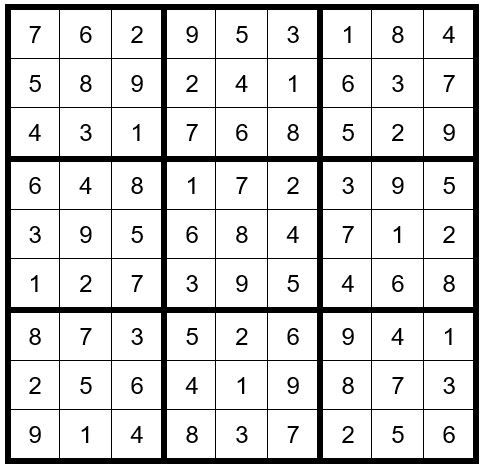
We see that the only cell in box 7 that can now be a 7 is C2R7.  C2R7=7.  Now you have a triplet 346 in column 2; therefore, C2R6=2.  C1R5=3.  C2R8=5.  C4R7=5, and so forth.  From this point the puzzle is easily solved.  Your final grid should now look like Example #49.11 below:

May the gentle winds of Sudoku be at your back,

Dan LeKander, Wellesley Island

Editor’s note:

In January 2016, we published a final article in his series – but many of us enjoy using “Dan’s Steps,” so when he asked if we would like a puzzle to solve every month … this editor said an enthusiastic… Yes, please! Now we are several years later and on Puzzle #49!

I suggest you purchase Dan’s book as a Christmas gift: “3 Advanced Sudoku Techniques, That Will Change Your Game Forever!”

The book is available online, amazon.com and on ebay.com.

Most importantly, I ask that you leave comments on any part of his series and throughout the year.  Remember when your teacher said – no such thing as a silly question – as we can all learn together.

As always, I want to thank Dan…and his proofreader… Peggy! I am hoping you will enjoy our Sudoku and at the same time join me in thanking Dan - Bravo to you both…

Posted in: Volume 14, Issue 2, February 2019, Sports