Puzzle #59 can be scary, but not if you learned an Advanced Technique.
DAN’S 8-STEP APPROACH TO SOLVING ALL SUDOKU PUZZLES
Once you have completed the puzzle, to the extent that you have filled-in all obvious answers and have written all potential options across the top of the unsolved cells (PUZZLE PREPARATION), Dan recommends the following Steps to complete the puzzle.
Step 1: Sudoku Pairs, Triplets and Quads – See September 2015
Step 2: Turbos & Interaction – See October 2015
Step 3: Sudoku Gordonian Rectangles and Polygons – See November 2015
Step 4: XY-Wings & XYZ Wings – See December 2015
Step 5: X-Wings – See January 2016
Step 6: DAN’S YES/NO CHALLENGE
Step 7: DAN’S CLOSE RELATIONSHIP CHALLENGE
Step 8: AN EXPANSION OF STEP 7
Steps 1-5 are relatively common techniques and are explained in the TI LIFE articles above. Steps 6-8 are covered in detail, in Dan’s book.
If we say 7 saves 6, those of you who have been following my articles will probably realize the meaning!
Let's get started!
PUZZLE PREPARATION:
Prior to utilizing techniques first complete the 5 Steps of Puzzle Preparation …
- FILL IN DATA FROM OBSERVATIONS
- FILL IN OBVIOUS ANSWERS
- FILL IN NOT-SO-OBVIOUS ANSWERS
- MARK UNSOLVED CELLS WITH OPTIONS THAT CANNOT EXIST IN THOSE CELLS
- FILL IN THE OPTIONS FOR THE UNSOLVED CELLS
This month we will again complete all of the first 4 steps in the order we observe them, versus all step 1, then step 2, step 3, and step 4 in order, before we move on to step 5.
We will start with the 1’s and navigate through 2’s to 9’s, then repeat the process until we conclude all step 1-4 clues.
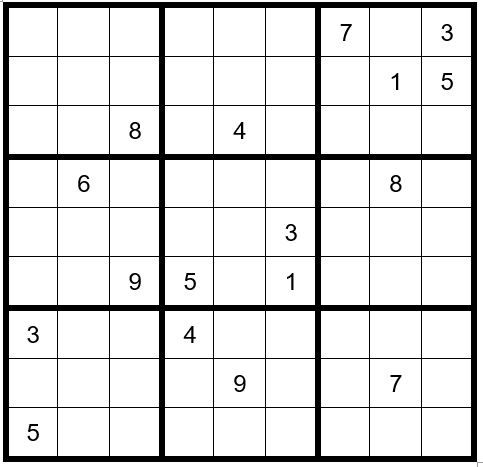
The first thing we observe is that C6R4 (cell in column 6, row 4) =4 (obvious answer). Then C7R2=8 & C8R1=4.
Now your grid should like Example #59.1 below:
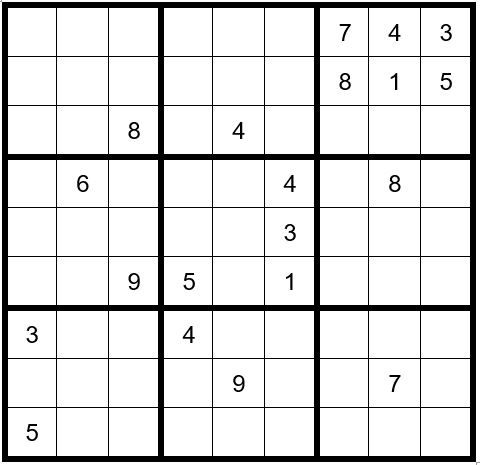
We know that C7R3, C8R3 & C9R3 are an obvious triplet 269, so fill in the options for those 3 cells.
The only cells in box 5 (middle box of 9 x 9 cells) that can be a 9 are C4R4 & C4R5; therefore, a 9 cannot exist in C4R1, C4R2 or C4R3. Indicate this by placing a small 9 in the bottom of those 3 cells.
We also realize the only unsolved cells in box 7 that can be a 9 are C2R7 & C2R9; therefore, a 9 cannot exist as an option in C2R1, C2R2 or C2R3.
Now your grid should look like Example #59.2 below:
We have now completed Puzzle Preparation steps 1-4, so we will fill in the options for the un-solved cells. Remember the obvious triplet in box 3, such that a 2, 6 or 9 cannot exist in any other unsolved cells in row 3. Now your grid should look like Example #59.3 below.
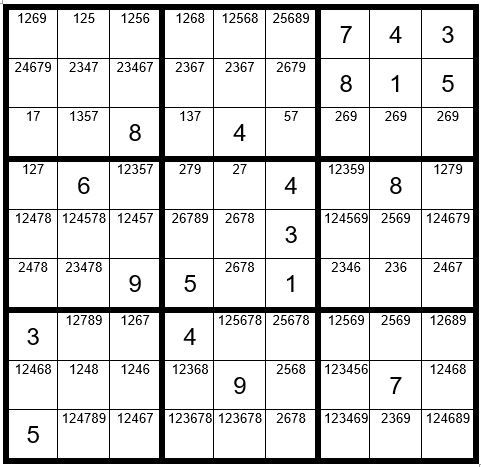
STEPS 1-5
Can you locate any pairs, triplets, quad or quints? In row 4 we see that the two options 35 only exist in the two cells C3R4 & C7R4, which is a hidden pair.
Now your grid should look like Example #59.4 below:
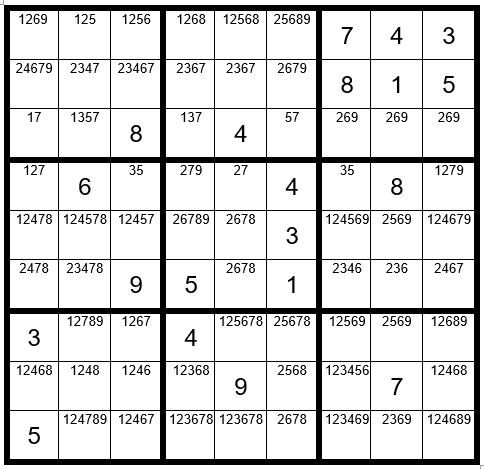
There are no additional Step 1-5 clues, so we will now proceed to Step 6: Dan’s Yes-No Challenge.
There are 3 circumstances that establish the potential for a Step 6 exercise:
- Look for just 2 unsolved cells in a box that contain the same option where these 2 cells are not in the same row or column.
- Look for just 2 unsolved cells in a column that contain the same option where these 2 cells are not in the same box.
- Look for just 2 unsolved cells in a row that contain the same option where these 2 cells are not in the same box.
We will start by searching the 1’s to see if there is a potential Step 6 clue, and then navigate through the 2-9’s.
In row 8 we find just two unsolved cells with option 3. We will call these two cells our “driver cells” which drive the exercise. One of these two cells must be a 3. We will first start with C4R8 and assume it is the 3, to see what effect it has on the other unsolved cells with option 3. Then, we will assume C7R8 is the 3, to see what effect it has on the other unsolved cells. We will annotate C4R8 with a “Y” for yes, and annotate C7R8 with “y” to indicate yes. Please refer to Example #59.5 below:
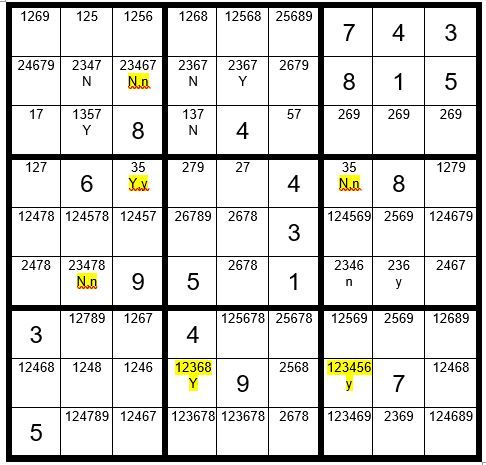
If C4R8=3, then C4R2 & C4R3 are not a 3 (marked as “N”) above. Now in box 2, C5R2 must be a 3 (Y). It follows that C2R2 & C3R2=N, C2R3=Y, C2R6=N, C3R4=Y and C7R4=N.
If C7R8=3, then C7R4 & C7R6=n, C8R6=y, C2R6=n, C3R4=y and finally C3R2=n.
Our conclusion is simple, the cells with the N,n designation are not a 3 regardless of which starter cell is a 3. The cell with the Y,y designation is a 3 regardless of which starter cell is a 3.
Now your grid should look like Example #59.6 below:
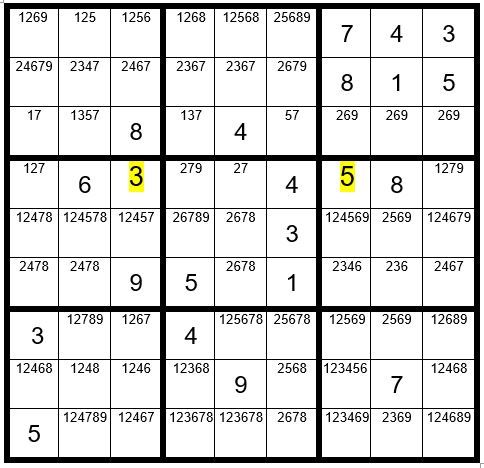
We see that C7R4=5. It then follows that C8R7=5, C6R8=5, C6R3=7, C1R3=1, C4R3=3, C2R3=5, C2R1=2, C3R1=6, C1R1=9, C2R2=3, C3R5=5, C6R1=8, and so forth. The puzzle is easily solved giving us the answer,
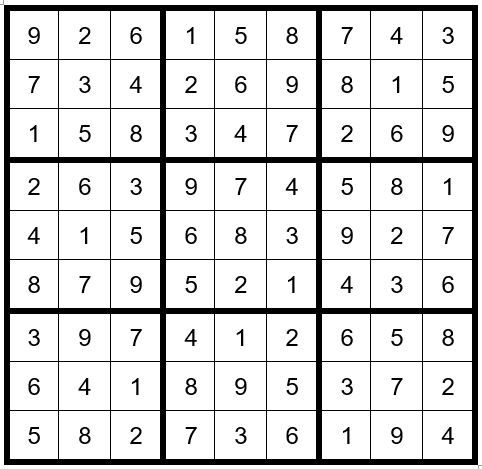
May the gentle winds of Sudoku be at your back.
By Dan LeKander, Wellesley Island
Editor's Note: It was back in January 2016, when we published a final article in Dan's series of steps to learn the logic of Sudoku – when he asked if we would like a puzzle to solve every month … this editor said an enthusiastic… Yes, please! Now we are several years later and on Puzzle #59. (How many have you solved... please let us know!)
If you have not already done so, I suggest you purchase Dan’s book: “3 Advanced Sudoku Techniques, That Will Change Your Game Forever!” Purchase of a book includes a 50-page blank grid pad, 33 black and two green tokens, to assist with Step 6.…

The book is available online at ebay.com.
Most importantly, I ask that you leave comments on any part of his series and throughout the year.
And now we are in October 2019... many puzzles later... I want to thank Dan…and his proofreader… Peggy! I am hoping you will enjoy our monthly Sudoku and at the same time join me in saluting Dan - Bravo to you both…(As I said last month - mind you sometimes I am not so polite when I can't solve the puzzle...)
Be sure to read the review of Dan's book by Jesse Kahn published in Jun 2015.
Also all past Sudoku Puzzle Challenge beginning: February 2016, March 2016, April 2016, May 2016, June 2016, July 2016, August 2016, September 2016, October 2016, November 2016, December 2016, January 2017, February 2017, March 2017 , April 2017, May 2017, June 2017, July 2017, August 2017, September 2017, October 2017, November 2017, December 2017, January 2018, February 2018, March 2018, April 2018.May 2018, June 2018, July 2018, August 2018, September 2018 , October 2018, November 2018, December 2018, January 2019, February 2019, March 2019, April 2019, May 2019 June 2019, July 2019, August, 2019 and September 2019.
Posted in: Volume 14, Issue 10, October 2019, Sports
Please click here if you are unable to post your comment.