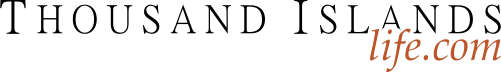Begin 2020 with a Sudoku Puzzle...
PUZZLE PREPARATION
Prior to utilizing techniques first complete the 5 Steps of Puzzle Preparation …
- FILL IN DATA FROM OBSERVATIONS
- FILL IN OBVIOUS ANSWERS
- FILL IN NOT-SO-OBVIOUS ANSWERS
- MARK UNSOLVED CELLS WITH OPTIONS THAT CANNOT EXIST IN THOSE CELLS
- FILL IN THE OPTIONS FOR THE UNSOLVED CELLS
This month we will again complete all of the first 4 steps in the order we observe them, versus all step 1, then step 2, step 3, and step 4 in order, before we move on to step 5.
We will start with the 1’s and navigate through 2’s to 9’s, then repeat the process until we conclude all step 1-4 clues.
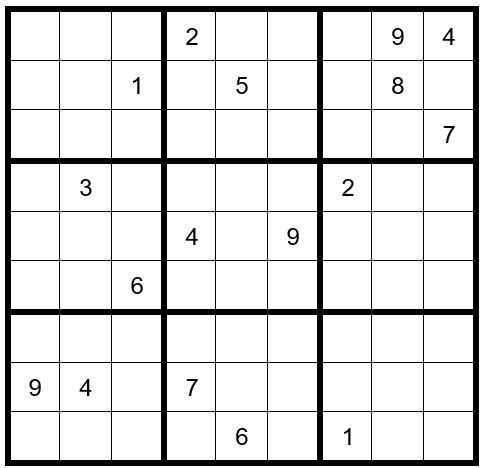
The first thing we observe is that C8R3 (cell in column 8, row 3) =1(obvious answer). Then, C9R2=2. Now the options for C7R1,2,3 are 356.
We will enter those in the top of the cells. The options for the remaining unsolved cells in column 7 are 4789. There is already a 479 in row 8; therefore, C7R8=8. There is already a 4 and 9 in row 5; therefore, C7R5=7. Now your grid should look like Example #62.1 below:
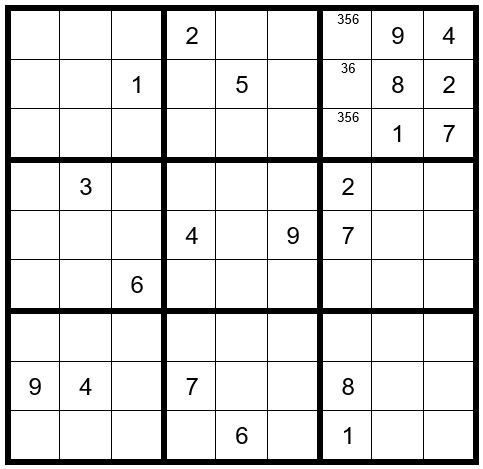
In box 5 a 6 can only exist as an option in C4R4 or C6R4; therefore, a 6 cannot exist in C8R4 or C9R4.
In box 7 the options 16 can only exist in C1R7 or C2R7. We will enter them now.
Now your grid should look like Example #62.1 below:
We have now completed Puzzle Preparation steps 1-4, so we will fill in the options for the un-solved cells. Please keep in mind that no other cells in box 7 or row 7 can have options 16. Al-so, please keep in mind the triplet 356 in column 7. Now your grid should look like Example #62.3 below:
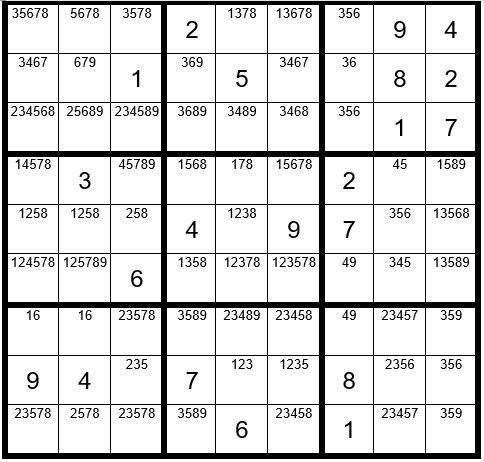
Can you locate any pairs, triplets, quads or quints?
In column 5 we see that the two options 49 only exist in the two cells C5R3 & C5R7, which is a hidden pair.
Now your grid should look like Example #62.4 below:
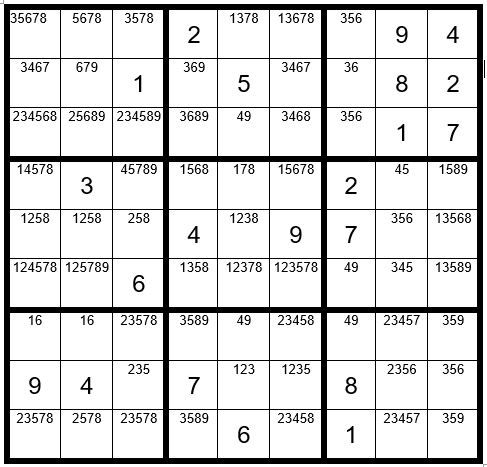
We now see that there is already another unsolved cell in row 7 with options 49, so you can remove the options 49 from any other cell in row 7. Now your grid should look like Example #62.5 below:
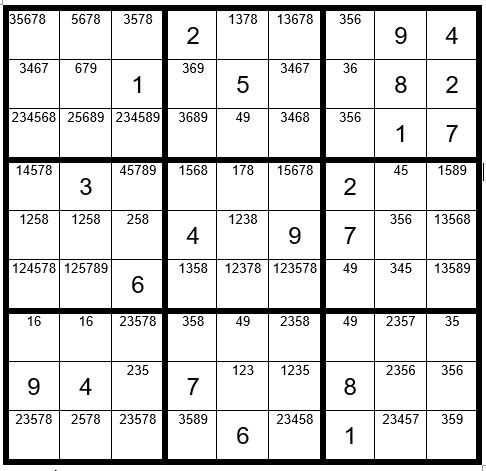
Can you spot any more pairs, triplets, quads or quints? Look carefully at column 3. Only two unsolved cells have options 49, which are C3R3 & C3R4. So, change those cells to “49”. You can also see that you can now remove any unsolved cells in row 3 that have options 4 or 9. Now your grid should look like Example #62.6 below:
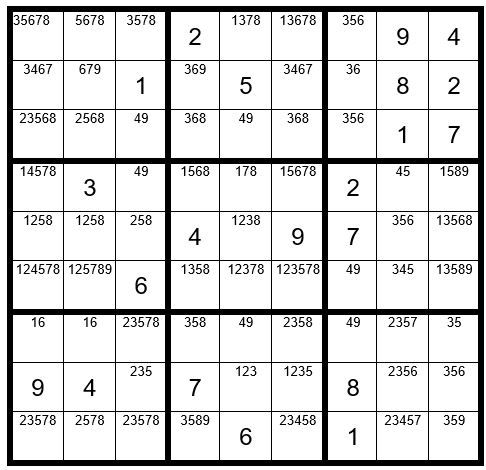
Can you locate any other clues before we proceed to advanced techniques? Yes, check out column 4. C4R4 & C4R6 are the only unsolved cells in column 4 with option 1. They are both contained in box 5; therefore, no other cells in box may contain the number 1 as an option (Interaction) , giving us Example #62.7 below:
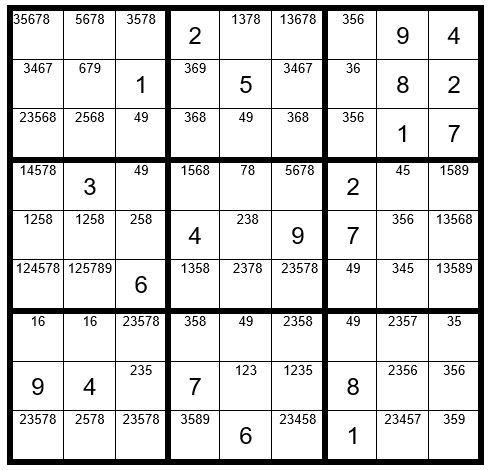
There are no additional Step 1-5 clues, so we will now proceed to Step 6: Dan’s Yes-No Challenge.
There are 3 circumstances that establish the potential for a Step 6 exercise:
- Look for just 2 unsolved cells in a box that contain the same option where these 2 cells are not in the same row or column.
- Look for just 2 unsolved cells in a column that contain the same option where these 2 cells are not in the same box.
- Look for just 2 unsolved cells in a row that contain the same option where these 2 cells are not in the same box.
We will start by searching the 1’s to see if there is a potential Step 6 clue, and then navigate through the 2-9’s.
In column 3 we find just two unsolved cells with option 9. We will call these two cells our “driver cells” which drive the exercise. One of these two cells must be a 9. We will first start with C3R3 and assume it is the 9, to see what effect it has on the other unsolved cells with option 9. Then, we will assume C3R4 is the 9, to see what effect it has on the other unsolved cells. We will annotate C3R3 with a “Y” for yes, and annotate C3R4 with “y” to indicate yes. Please refer to Example #62.8 below:
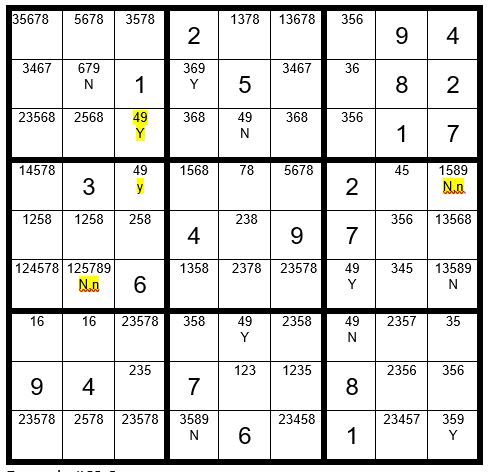
Looking at the example above, if C3R3=9, then C2R2 & C5R3 are not a 9 (marked as “N”) above. Now C4R2 must be a 9 (Y). It follows that C4R9=N. C5R7=Y. C7R7=N. C7R6=Y. C9R4=N. C9R6=N. C2R6=N. C9R9=Y.
If C3R4=9, then C2R6=n. C9R4=n.
Our conclusion is simple, the two cells with the N,n designation are not a 9 regardless of which starter cell is a 9. Since C2R6 is not a 9, then the only cell In box 4 that can be a 9 is C3R4. C3R4=9.
Now your grid should look like Example #62.9 below:
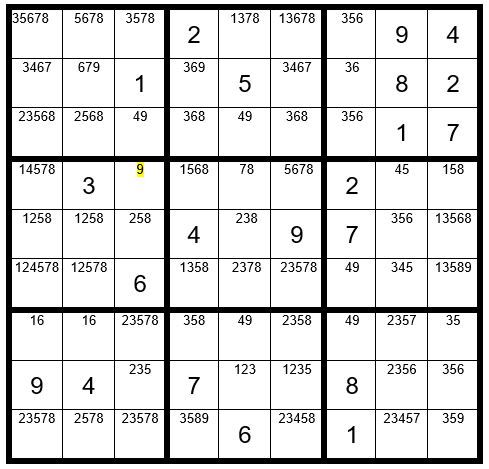
It now follows that C3R3=4, C5R3=9, C5R7=4, C7R7=9, C7R6=4, C8R4=5, C8R6=3, C8R5=6 and so forth, leading to an easy completion as per Example #62.10 below:
In an effort to promote Sudoku and its creative problem-solving benefits, I would enjoy gifting books in bulk to teachers who wish to use the book in their classrooms. Additionally, I would enjoy gifting copies to senior centers and assisted living homes. As I have a limited supply please respond soon to be included. Please send requests to my e-mail …djlsuniverse@yahoo.com
May the gentle winds of Sudoku be at your back.
By Dan LeKander
Editor's Note:
First, we thank you Dan for your generous offer. Each month I write that it was back in January 2016, when we published a final article in Dan's series of steps to learn the logic of Sudoku – that he asked if we would like a puzzle to solve every month … this editor said an enthusiastic… Yes, please! Now we are several years later and on Puzzle #62.
If you have not already done so, I suggest you purchase Dan’s book: