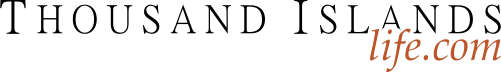Greetings friends of the River. Get your Sudoku hat, hot cup of coffee and a sharp pencil ready for the April Sudoku puzzles.
Clueless?
As a bonus each month this year we will start with a Sudoku puzzle in progress, where it appears there are no more obvious or not-so-obvious clues. Does this puzzle #79 have any more clues?
(The answer follows below after the conclusion of Puzzle #80, the feature puzzle for April)
The Impossible Series continues. See if you can solve this puzzle without any assistance!
DAN’S 8-STEP APPROACH TO SOLVING ALL SUDOKU PUZZLES
Once you have completed the puzzle, to the extent that you have filled-in all obvious answers and have written all potential options across the top of the unsolved cells (PUZZLE PREPARATION), Dan recommends the following Steps to complete the puzzle.
Step 1: Sudoku Pairs, Triplets and Quads – See September 2015
Step 2: Turbos & Interaction – See October 2015
Step 3: Sudoku Gordonian Rectangles and Polygons – See November 2015
Step 4: XY-Wings & XYZ Wings – See December 2015
Step 5: X-Wings – See January 2016
Step 6: DAN’S YES/NO CHALLENGE
Step 7: DAN’S CLOSE RELATIONSHIP CHALLENGE
Step 8: AN EXPANSION OF STEP 7Steps 1-5 are relatively common techniques and are explained in the TI LIFE articles above. Steps 6-8 are covered in detail, in Dan’s book.

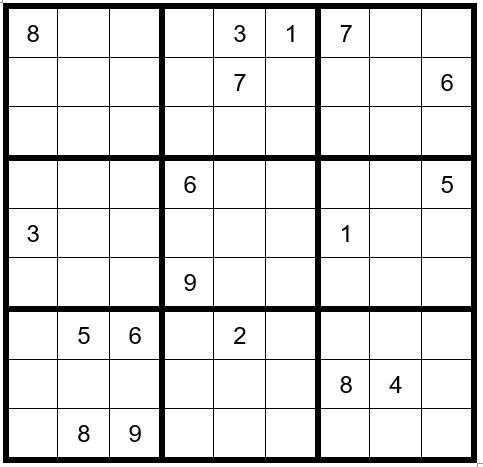
Puzzle #80
PUZZLE PREPARATION
Prior to utilizing techniques 1-8 first complete the 5 Steps of Puzzle Preparation …
- FILL IN DATA FROM OBSERVATIONS
- FILL IN OBVIOUS ANSWERS
- FILL IN NOT-SO-OBVIOUS ANSWERS
- MARK UNSOLVED CELLS WITH OPTIONS THAT CANNOT EXIST IN THOSE CELLS
- FILL IN THE OPTIONS FOR THE UNSOLVED CELLS
We will complete all of the first 4 steps in the order we observe them.
We will start with the 1’s and navigate through 2’s to 9’s, then repeat the process until we conclude all Puzzle Preparation Step 1-4 clues.
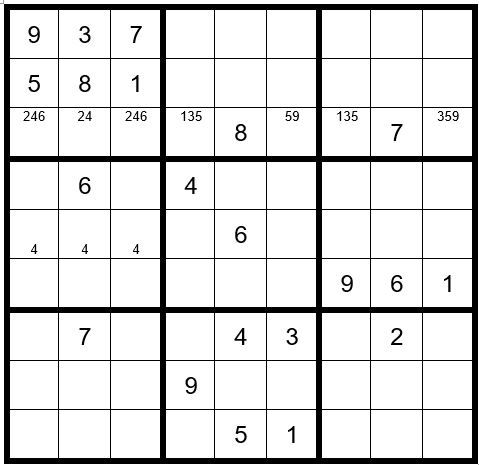
The first thing we observe is that C8R6 (cell in column 8, row 6) =6 (obvious answer). Then, C3R1=7 and C2R2=8. Looking at C5R7 we see the only number it can be is a 4. Fill in the options for the remaining three cells in box 1. Now the remaining unsolved cells in row 3 can have only options 1,3,5 and 9. Fill in the options for those four cells.
Now your grid should look like Example #80.1 below:
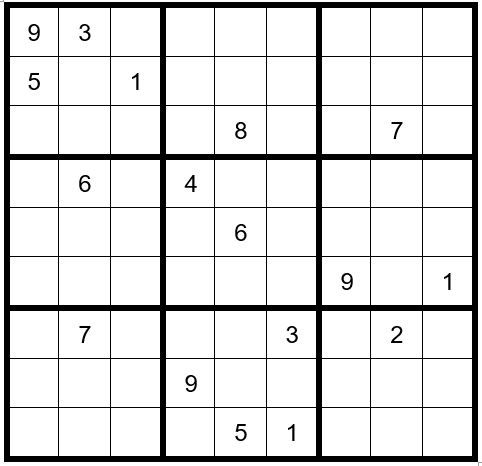
In box six a 4 can only exist as an option in C7R5, C8R5 or C9R5; therefore, a 4 cannot exist as an option in C1R5, C2R5 and C3R5. Indicate this by placing a small 4 in the bottom of those cells.
Now your grid should look like Example #80.2 below:
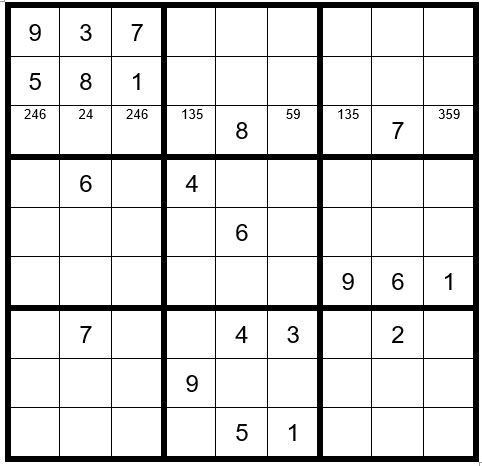
This concludes Puzzle Preparation steps 1-4. We will now fill in the options for the unsolved cells, giving us Example #80.3 below:
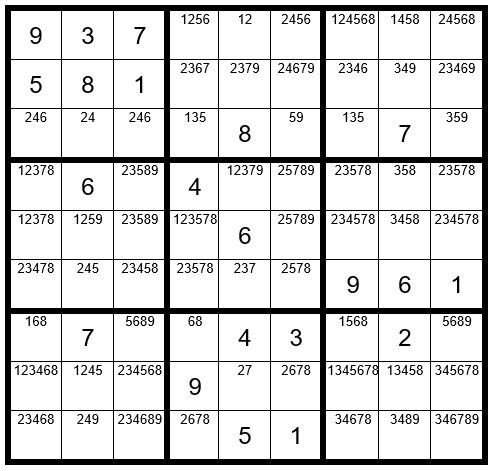
TECHNIQUES 1-5
There are no other Step 1-5 clues.
We will now proceed to Step 6: Dan’s Yes-No Challenge. We will start by searching the 1’s to see if there is a potential Step 6 clue, and then navigate through the 2-9’s.
There are 3 circumstances that establish the potential for a Step 6 exercise:
- Look for just 2 unsolved cells in a box that contain the same option where these 2 cells are not in the same row or column.
- Look for just 2 unsolved cells in a column that contain the same option where these 2 cells are not in the same box.
- Look for just 2 unsolved cells in a row that contain the same option where these 2 cells are not in the same box.
In Example #80.4 below we find two unsolved cells in column 4 that are not in the same box having a 1 as an option, C4R3 & C4R5 which become our “driver” cells. One of these two cells must be a 1.
We start with C4R3 and assume it is the 1 and assign a “Y”. We then mark, as before in previous month article Step 6 exercises, the cells which can and cannot be a 1 with the Y’s and N’s. We then assume C4R5 is the 1 and assign a “y”. We then mark the cells which can and cannot be a 1 with the y’s and n’s. Where we see a N,n indicates a cell that cannot be an 1 regardless of whether C4R3 or C4R5 is the 1 in column four.
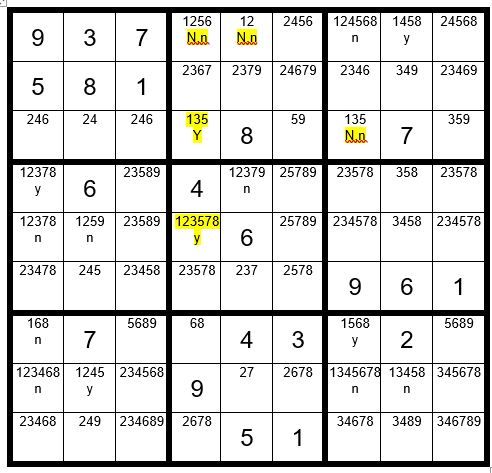
We can see from the exercise above that three cells have N,n designations, thus, they cannot have a 1 as an option. We also see that the only cell in box 2 that can now be a 1 is C4R3. Thus, C4R3=1. We will make those changes, giving us Example #80.5 below:
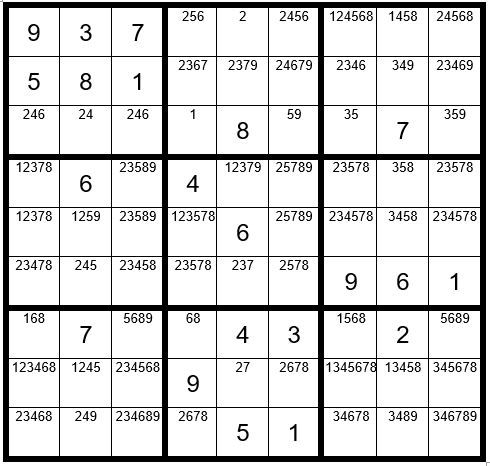
We can see from the example above that C5R2=2. We can also see that C5R4=1, C5R8=7, C5R6=3 and C5R2=7. From this point the puzzle is easily solved, giving us the Example 80.6 below:
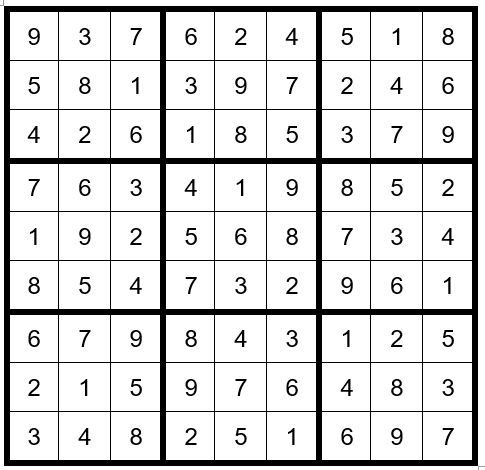
Let’s pause here to ask ourselves some questions. When searching for a Step 6 prospect in a puzzle is there an optimum number of given answers of numbers 1 through 9 that will en-hance a successful outcome? In the puzzle above, we chose the number 1 to perform a Step 6 exercise.
How many completed cells were number 1? In this case, three cells had number one as the answer. This brings up the next question. How often is a successful Step 6 per-formed with three cells containing the number chosen for the exercise?
To answer that question, I looked at all the articles in the last 16 months that contained a Step 6 exercise. Out of the 16 monthly articles, 11 had Step 6 exercises. Out of those 11, all 11 had three given an-swers for the digit chosen! This brings up the next logical question.
Why are 3 given an-swers such a magical number? Essentially, once you find a potential Step 6 exercise you have to track the “yes” and “no” cells through the puzzle. If you have less than 2 given answers or more than 3 given answers for the digit, the track will generally not be productive. So, the next time you perform a Step 6 exercise, check the digits 1-9 that have 3 given answers first.
May the gentle winds of Sudoku be at your back.
By Dan LeKander
Clue for Puzzle #79 … focus your attention to row 1. What do you observe?
There is only one cell in row 1 that can have a 6 as an option. C2R1=6. It follows that C1R6=6, C8R5=6 and C7R9=6.
Editor's Note: Can't believe #80... Dan and his proofreader (and, as they say, better half) Peggy, give us a new challenge each month.
I copy the article - insert the examples and then realize just how much work goes into each one of the Dan's articles. I have the easy job, his is difficult and then you, our readers, have the challenge.
It was back in January 2016, when we published a final article in Dan's Series of Steps to learn the logic of Sudoku – he asked if we would like a puzzle to solve every month … this editor said an enthusiastic… Yes, please!
If you have not already done so, I suggest you purchase Dan’s book: