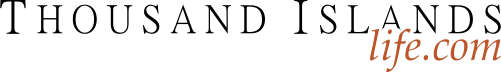A special treat awaits you this month. The “Clueless?” series continues, challenging you to think outside the box! Did I really mean that? You be the judge. And to fulfill the theme of February, we have a sweetheart of a puzzle for you. Please enjoy.
Clueless?
Each month this year we will start with a Sudoku puzzle in progress, where it appears there are no more obvious or not-so-obvious clues. Does this puzzle #75 have any more clues? The answer is obviously yes. Can you find the clue?
The answer follows at the end of the article after the conclusion of the feature puzzle for February, #76.
____________________________
DAN’S 8-STEP APPROACH TO SOLVING ALL SUDOKU PUZZLES
Once you have completed the puzzle, to the extent that you have filled-in all obvious answers and have written all potential options across the top of the unsolved cells (PUZZLE PREPARATION), Dan recommends the following Steps to complete the puzzle.
Step 1: Sudoku Pairs, Triplets and Quads – See September 2015
Step 2: Turbos & Interaction – See October 2015
Step 3: Sudoku Gordonian Rectangles and Polygons – See November 2015
Step 4: XY-Wings & XYZ Wings – See December 2015
Step 5: X-Wings – See January 2016
Step 6: DAN’S YES/NO CHALLENGE
Step 7: DAN’S CLOSE RELATIONSHIP CHALLENGE
Step 8: AN EXPANSION OF STEP 7Steps 1-5 are relatively common techniques and are explained in the TI LIFE articles above. Steps 6-8 are covered in detail, in Dan’s book.

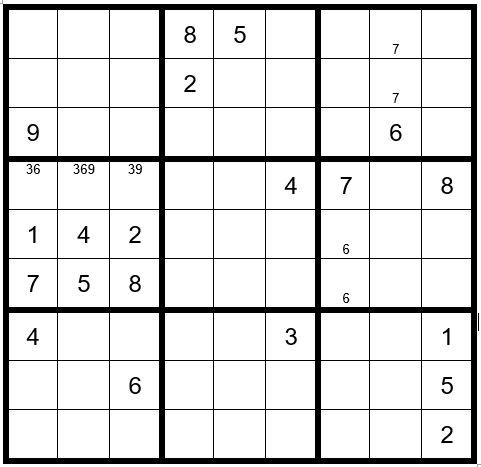
Off we go with Puzzle #76, a sweetheart of a puzzle. You may ask why it is a sweetheart. Once we start applying our techniques, you will see that this puzzle brilliantly illustrates the power of a technique, more so than any other puzzle I have explored.
Puzzle #76
PUZZLE PREPARATION
Prior to utilizing techniques first complete the 5 Steps of Puzzle Preparation …
- FILL IN DATA FROM OBSERVATIONS
- FILL IN OBVIOUS ANSWERS
- FILL IN NOT-SO-OBVIOUS ANSWERS
- MARK UNSOLVED CELLS WITH OPTIONS THAT CANNOT EXIST IN THOSE CELLS
- FILL IN THE OPTIONS FOR THE UNSOLVED CELLS
We will complete all of the first 4 steps in the order we observe them.
We will start with the 1’s and navigate through 2’s to 9’s, then repeat the process until we conclude all Puzzle Preparation Step 1-4 clues.
The first thing we observe is that C3R6 (cell in column 3, row 6) =1 (obvious answer). Then, C8R5=1, C7R8=1, C5R9=1, C6R3=1, and C2R2=1. That concludes the 1’s. C8R3=8, C3R1=8, C1R8=8, C5R7=8, C4R6=8, and C9R4=8. That concludes the 8’s. C8R2=6, C5R3=9, C9R9=9. Well, that went smoothly, but a danger sign should start to show. We will soon see that the remaining unsolved cells will have multiple options, mostly all greater than two. And steps 7 & 8 depend on unsolved cells with only two options.
Now your grid should look like Example #76.1 below:
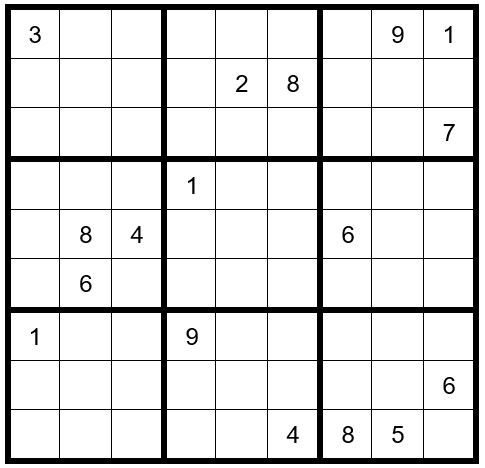
In box two a 3 can only exist as an option in C4R2 or C4R3; therefore, a 3 cannot exist as an op-tion in C4R5, C4R8 or C4R9. Indicate this by placing a small 3 in the bottom of those cells.
In box seven a 4 can only exist as an option in cells C2R7 or C2R8; therefore, a 4 cannot exist as an option in C2R1 or C2R2.
In box one a 6 can only exist as an option in cells C1R3 or C3R3; therefore, a 6 cannot exist as an option in C4R3.
In box four a 3 can only exist as an option in cells C2R4 & C3R4; therefore, a 3 cannot exist as an option in C5R4, C6R4, C7R4 & C8R4.
In box three a 2 can only exist as an option in cells C7R1 or C7R3; therefore, a 2 cannot exist as an option in C7R4, C7R6 & C7R7.
Now your grid should look like Example #76.2 below:
Example #76.2
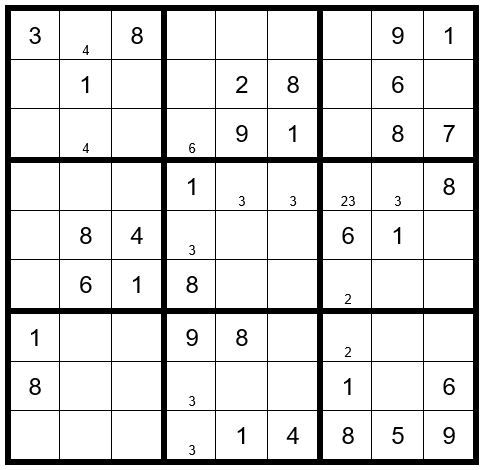
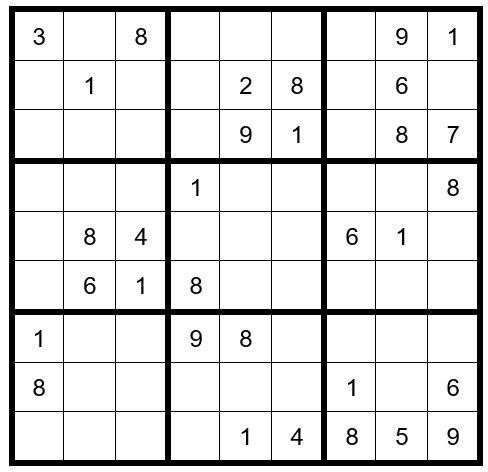
This concludes Puzzle Preparation steps 1-4. We will now fill in the options for the unsolved cells, giving us Example #76.3 below:

TECHNIQUES 1-5
We find an Interaction in box 7. A 3 has to exist as an option in C2R9 or C3R9; therefore, a 3 cannot exist as an option for any other cell in box 7. Now your grid should look like Example #76.4 below:

There are no additional Step 1-5 clues, and there are no productive Step 6 clues, so we will move on the Step 7, Dan’s Close Relationship Challenge. Hopefully, you remember a Step 7 exercise requires a 2-digit unsolved cell to be a driver cell. In our puzzle above, there is only one unsolved cell with 2 digits, C2R3. I tried sequences 2,5 and 5,2 and neither would track far enough through the puzzle to provide any clues.
We find ourselves in a bit of a pickle. What do we do? As our last opportunity we hope Step 8, An Expansion of Dan’s Close Relationship Challenge will provide a clue.
First, we will define the prerequisites for a Step 8. You must find a 3-digit option unsolved cell and a 2-digit unsolved cell in the same box, column or row that have 2 numbers in common. We will choose C2R1 & C2R3 and highlight the options of those two cells in green as per Example #76.5 below:

The 3-digit cell C2R1 is the driver cell, and we must pick a sequence to get this started. Here is a hint, the sequence always starts with the options of the 2-digit cell, in this example, the 2 and 5 in C2R3. We finalize the sequence as 2,5,7 and enter this on level 2 of the driver cell, per example above.
Let’s explore the logic. If C2R1 is a 2, then C1R3, C3R3, C2R4, C2R7, C2R8 & C2R9 cannot be a 2. If C2R1 is a 5, then C2R3 is a 2 and the same cells cannot be a 2. We will mark those six cells as N2 in the example above on the 2nd level of the cells.
If C2R1 is a 5, then C1R2, C1R3, C3R2, C3R3, C2R4, C2R7, & C2R8 are not a 5. If C2R1 is a 2, then C2R3 is a 5 and those same cells cannot be a 5. We will mark those 7 cells as N5 in the example above on the 2nd level of the cells.
Let’s pause and explore the logic. We will track the 7 in C2R1 through the puzzle to see if we can establish what the resulting number would be for the cells with N25 and N5. To illustrate, we will create a hypothetical situation.
Say C3R3 ends up being a 6. What will we know about the cell? OK, if C2R1 is a 2, then we know C3R3 is not a 2. If C2R1 is a 5, then we know C2R3 is a 2 and therefore, C3R3 is not a 2. And if C2R1 is a 7, then in this situation we would know C3R3 is not a 2 regardless of which number 2, 5, or 7 that C2R1 really is. And we could elimi-nate the 2 from C3R3 as an option. The same logic could be applied with the N5, and in this case, the 5 could be eliminated from C3R3 as an option, which would mean C3R3 has to be a 6.
We will now track the 7 in C2R1 through the puzzle to actually see what happens, per Example #76.6 below:
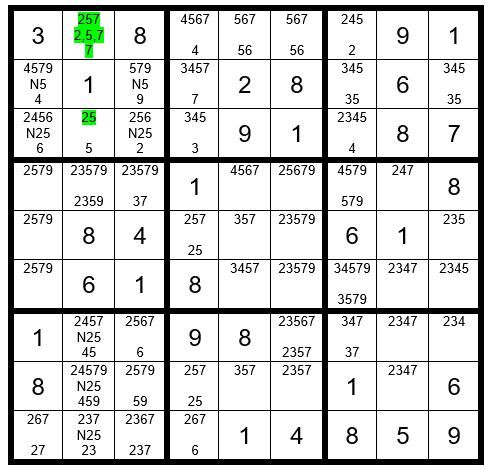
We will track the 7 in the 3rd level of each unsolved cell to preserve the integrity of the original puzzle. C2R1 being a 7 means C5R1 & C6R1 now have options 56, and therefore, C4R1 is a 4, C7R1 is a 2, C4R3 is a 3, and C4R2 is a 7. C4R9 is a 6. Now C1R9 has options 27, C2R9=23 and C3R9 is 237. This is a triplet, and a 2,3 and 7 cannot exist in any other unsolved cell in box 7. We have now found our first clue. C2R7 and C2R8 are not a 2 regardless if C2R1 is a 2, 5 or 7. So, we could eliminate the 2 from those two cells as an option, which we will do when we complete the track of the 7 through the puzzle.
We see a pair, 59 in C3R2 and C3R8; therefore, C3R7=6. C3R3=2. We now have our second clue. C3R3 is not a 5 regardless if C2R 1 is a 2, 5 or 7, and the 5 can later be removed as an op-tion from C3R3.
C1R3=6. This tells us C1R3 cannot be a 2 or 5 regardless of the value of C2R1, and later the op-tions 2 and 5 can be eliminated from C1R3.
C2R3=5. C3R2=9 and C1R2=4. More clues have surfaced.
We will continue the track in Example #76.7 below:
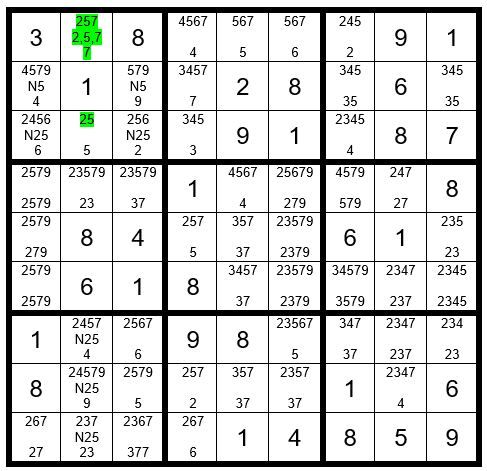
Continue with the track of C2R1 being a 7. C3R8=5, C2R7=4 (more clues), C2R8=9 (more clues), C6R7=5, C6R1=6, C5R1=5, C4R8=2, C4R5=5, C8R8=4, C5R4=4. We will pause here to see what is happening. Look at column 5, what do you notice? Three unsolved cells have op-tions 37. This is obviously a conflict. This tells us that C2R1 is not a 7. We will now “clean up” the puzzle in Example #76.8 below:
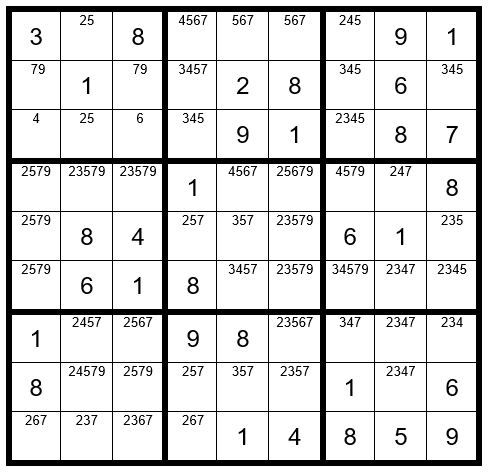
First, we will eliminate the 7 from C2R1. Now we have a pair with C2R1 and C2R3, and the 2 and 5 can be removed as options from all other unsolved cells in box 1 and column 2. That leaves C3R3=6 and C1R3-=4. The puzzle is easily solved from this point, giving you the completed puzzle, Example #76.9 below:
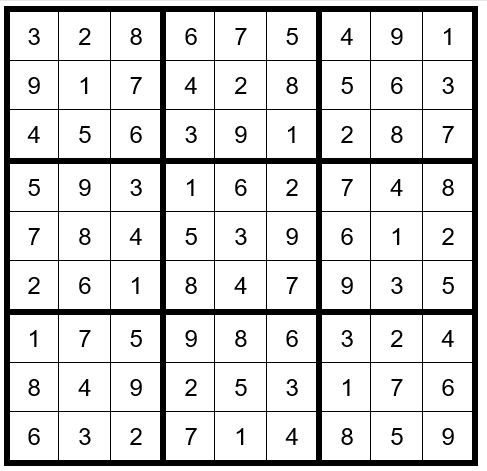
In this example, tracking the 7 in C2R1 created a conflict. There are a host of other possible outcomes of a Step 8 exercise. For example, the tracking could have abruptly ended, without a conflict. Given that outcome in this example, you still would have had options to delete, creating some 2-digit unsolved cells. Then you could have employed Step 7. Another outcome would have been a complete track through the puzzle without a conflict. This would have indicated that C2R1 was 7, and you have solved the puzzle.
If you think this is difficult, I agree. However, once you understand the logic, you can always refer to past examples to employ the correct tactics. You may not need this step often, but when you do, it is nice to have a “fall back” technique.
May the gentle winds of Sudoku be at your back.
Dan LeKander, Wellesley Island
Clue for Puzzle #75 … focus your attention to row 3. What do you observe?
4 unsolved cells in row three, specifically, C4R3, C5R3, C6R3 & C9R3 cannot be a 2,5 or 8. This means the options 2,5 & 8 can only exist in the 3 remaining unsolved cells in row 3, C2R3, C3R3 & C7R3. We notice that column three already has a 2 and 8 in it; therefore, it leaves C3R3 with a 5 as its only choice. Then the 5’s are easily dispatched, and the puzzle poses no difficulty in solving.
Editor's Note: We started January with two puzzles and we do again this month. #75 and #76!
Each month I copy the article - insert the examples and then shake my head as I realize just how much work goes into each one of the Dan's articles. I have the easy job, his is difficult and then you, our readers, have the challenge.
It was back in January five years ago in 2016, when we published a final article in Dan's Series of Steps to learn the logic of Sudoku – he asked if we would like a puzzle to solve every month … this editor said an enthusiastic… Yes, please!
If you have not already done so, I suggest you purchase Dan’s book: