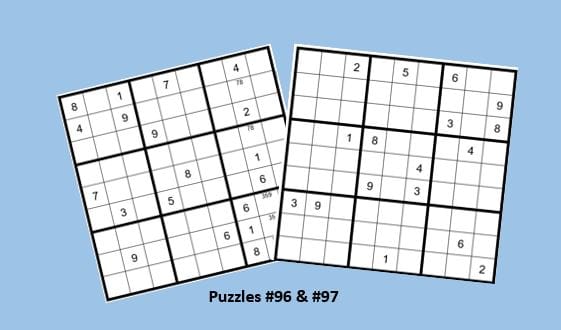
Sudoku Puzzle #96 & #97
by: Dan LeKander
Clueless?

As a bonus each month we start with a Sudoku puzzle in progress, where it appears there are no more obvious or not-so-obvious clues. Can you find the missing clue in Puzzle #96?
(The answer follows after the conclusion of Puzzle #97, the feature puzzle for December)
Feature Puzzle
This “impossible” puzzle #97 below reinforces the concept presented last month for solving Step 6 exercises without filling in the options for the unsolved cells. If you did not read that article, please click on and read the November 2021 article.

DAN’S 8-STEP APPROACH TO SOLVING ALL SUDOKU PUZZLES
Once you have completed the puzzle, to the extent that you have filled-in all obvious answers and have written all potential options across the top of the unsolved cells (PUZZLE PREPARATION), Dan recommends the following Steps to complete the puzzle.
Step 1: Sudoku Pairs, Triplets and Quads – See September 2015
Step 2: Turbos & Interaction – See October 2015
Step 3: Sudoku Gordonian Rectangles and Polygons – See November 2015
Step 4: XY-Wings & XYZ Wings – See December 2015
Step 5: X-Wings – See January 2016
Step 6: DAN’S YES/NO CHALLENGE
Step 7: DAN’S CLOSE RELATIONSHIP CHALLENGE
Step 8: AN EXPANSION OF STEP 7Steps 1-5 are relatively common techniques and are explained in the TI LIFE articles above. Steps 6-8 are covered in detail, in Dan’s book.

PUZZLE PREPARATION
Prior to utilizing Steps 1-8, complete the 5 Steps of Puzzle Preparation …
- FILL IN DATA FROM OBSERVATIONS
- FILL IN OBVIOUS ANSWERS
- FILL IN NOT-SO-OBVIOUS ANSWERS
- MARK UNSOLVED CELLS WITH OPTIONS THAT CANNOT EXIST IN THOSE CELLS
- FILL IN THE OPTIONS FOR THE UNSOLVED CELLS
We will complete all of the first 4 steps in the order we observe them, until we conclude all Puzzle Preparation Step 1-4 clues.
The first thing we observe is that C4R5=1. C6R4=5. C1R8 & C2R8 have options 12. C5R4, C5R5 & C5R6 have options 267. These clues give us Example #97.1 below:

So now, before we complete step 5 by filling in the options for all the unsolved cells, we will look at the puzzle and ask if there are any good Step 6 potentials. As in previous articles, we determined a particular number was a potentially successful Step 6 exercise if that number appears as a given answer in 3 separate boxes, such that the boxes are not side-by-side, nor over each other. Which numbers are good candidates? Yes, 3 and 9.
We will first pick the number 3 and perform the exercise. At this point at your home, you would put green tokens on two starter cells that are 3’s and black tokens on all unsolved cells that could have the option 3. For purposed of illustration, in Example #97.2 below we will highlight two starter cells in green, and the unsolved cells that could be a 3 in yellow (vs black).

Now we will perform the exercise.
We will use C3R2 and C3R5 as our starter cells. We will start with C3R2 and assume it is the 3. Then we can see that C4R2 & C5R2 cannot be a 3, then C4R1=3, C4R8 & C4R9 cannot be a 3, then C5R8=3, C9R8 cannot be a 3, C8R9=3, and C8R5 cannot be a 3.
Next, we assume that C3R5 is the 3. It follows that C8R5 & C9R5 cannot be a 3, then C9R4=3, then C9R8 cannot be a 3, then C8R9=3, then C4R9 cannot be a 3. So regardless of which starter cell is a 3, C4R9, C8R5 & C9R8 cannot be a 3, and regardless of which starter cell is a 3, C8R9=3.
It follows that a 9 can only exist as an option in C7R8 or C7R9, so, C7R4, C7R5 & C7R6 cannot be a 9; therefore, C8R5=9. The 9’s are quickly dispatched, and then the 3’s, leading to an easy conclusion per Example #97.3 below …

May the gentle winds of Sudoku be at your back.
Dan LeKander
Clue for Puzzle #96 … did you find the clue? If not, read on.
Let’s look at row 8. We see that C1R8 cannot have options 7 or 8, and neither can C5R8 or C8R8. This leaves the two unsolved cells C3R8 & C4R8 as the only two unsolved cells that can have options 78. We know that C1R2=4; therefore, the only cell in row 8 that can now be a 4 is C5R8. C5R8=4.
Editor's Note: December 2021!
Dan's fishing season has moved to the sunny south, but you can see from Puzzles #96 & #97 he is still creating puzzles for TI Life readers. Thanks Dan and your wonderful proofreader (and, as they say, better half) Peggy, once again you have given us a nice challenge.
It was back in January 2016, when we published a final article in Dan's Series of Steps to learn the logic of Sudoku – he asked if we would like a puzzle to solve every month . . . this editor said an enthusiastic - Yes, please!
If you have not already done so, I suggest you purchase Dan’s book: