Sudoku Puzzle #72
by: Dan LeKander
T. I. LIFE PUZZLE FOR DECEMBER 2020
In just over two weeks we will be saying hello to 2021. Let’s hope that the new year will bring us peace, harmony and good health.
DAN’S 8-STEP APPROACH TO SOLVING ALL SUDOKU PUZZLES
Once you have completed the puzzle, to the extent that you have filled-in all obvious answers and have written all potential options across the top of the unsolved cells (PUZZLE PREPARATION), Dan recommends the following Steps to complete the puzzle.
Step 1: Sudoku Pairs, Triplets and Quads – See September 2015
Step 2: Turbos & Interaction – See October 2015
Step 3: Sudoku Gordonian Rectangles and Polygons – See November 2015
Step 4: XY-Wings & XYZ Wings – See December 2015
Step 5: X-Wings – See January 2016
Step 6: DAN’S YES/NO CHALLENGE
Step 7: DAN’S CLOSE RELATIONSHIP CHALLENGE
Step 8: AN EXPANSION OF STEP 7Steps 1-5 are relatively common techniques and are explained in the TI LIFE articles above. Steps 6-8 are covered in detail, in Dan’s book.

To close out 2020 with the Sudoku articles, I realized that over the last five years of monthly Sudoku articles, there has not been an occasion to introduce a puzzle requiring Step 8, which is “An Expansion of Dan’s Close Relationship Challenge”. Recently while solving an “extreme” puzzle, it required Step 8, so I would like to share this technique with you. We’ll also break from our normal format. We will start with the original puzzle, but rather than go into detail, we will then jump to the point where Step 8 is required to solve the puzzle.
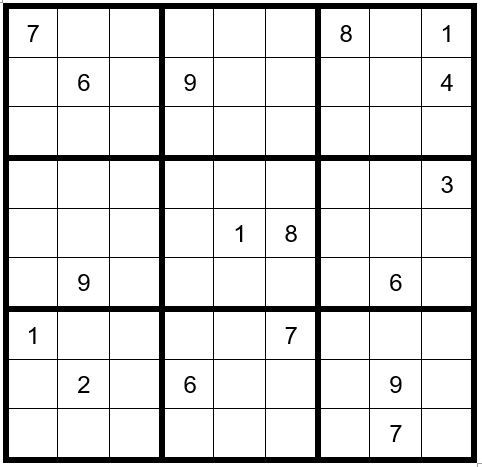
You are invited to see if your progress with Puzzle #72 matches this puzzle at the point of needing Step 8, which is Example #72.1 below:
Hint … if your puzzle looks like Example #72.1 except you have as options for C6R9 as 2345, then you missed a Step 6 with unsolved cells C2R1 & C2R7, eliminating the 4 as an option in C6R9.
Looking at the example above you see that the unsolved cells have some combination of just five numbers, 23458. This means that the grid is complete for numbers 1, 6, 7 & 9. This adds to the complexity of the puzzle at this point.
To the best of my inspection steps 1-7 are exhausted, and we must now turn to Step 8.
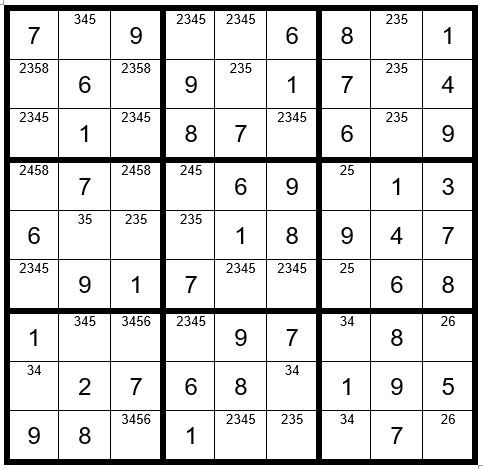
First, we will define the prerequisites for a Step 8. You must find a 3-digit option unsolved cell and a 2-digit unsolved cell in the same box, column or row that have 2 numbers in common. We will choose C4R4 & C7R4 and highlight the options of those two cells in green as per Example #72.2 below:
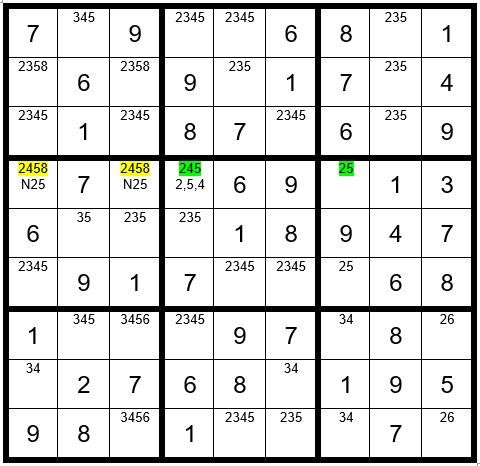
The driver cell is C4R4. We will select a sequence 2,5,4. C1R4 & C3R4 both contain options 2, 4 & 5 and are adjacent cells to the both green cells. Here is the logic:
• If the driver cell is a 2, then the yellow cells cannot be a 2
• If the driver cell is a 5, then C7R4 is a 2, and therefore, the yellow cells cannot be a 2. We will annotate the two yellow cells with N2, meaning regardless if C4R4 is a 2 or 5, the yellow cells cannot be a 2.
• If the driver cell is a 5, then the yellow cells cannot be a 5
• If the driver cell is a 2, then C7R4 is a 5, and therefore, the yellow cells cannot be a 5. We will annotate the two yellow cells with N5, meaning regardless if C4R4 is a 5 or 2, the yellow cells cannot be a 5.
So, what does this mean? We will assume the driver cell is a 4. If the tracking can tell us the value of the yellow cells when the driver cell is a 4, then we can make a deduction. Let’s say C1R4 turns out to be an 8. We would know that regardless if the driver cell is a 2, 5 or 4, that C1R4 is not a 2 or 5 and those options could be removed as an option from that cell. Or if C1R4 turns out to be a 2 we will know C1R4 cannot be a 5, and the 5 could be removed as an option from that cell.
We will now track the driver cell through the puzzle assuming it is a 4 and see what happens. Please refer to Example #72.3 below:
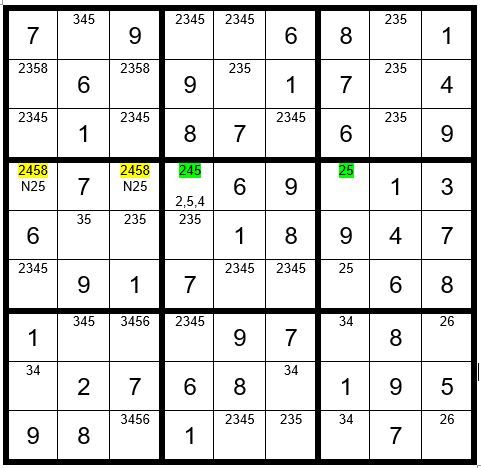
If C4R4 is a 4, then C1R6=4, C1R8=3, C6R8=4, C5R1=4, C3R3=4, C2R7=4, C7R7=3, and C7R9=4. We will pause here to bring the original puzzle down to the 3rd level of each unsolved cell to preserve the integrity of the current state of the original puzzle per Example #72.4 below:
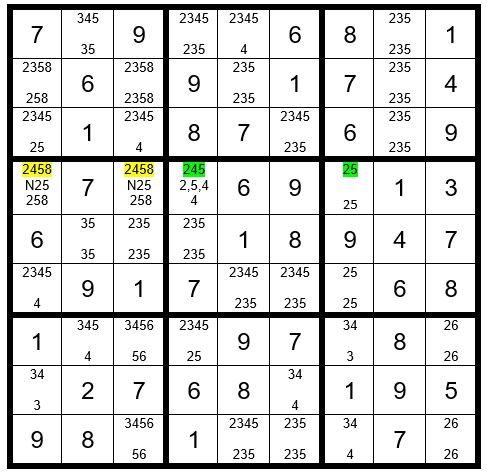
There are two key observations above. First, C3R7 & C3R9 have options 56, an obvious pair. That means any other unsolved cell in column 3 cannot have a 5 as an option. This tells us that regardless of which option is correct for the driver cell C4R4, C3R4 cannot have a 5 as an option and that option can be eliminated from C3R4. Secondly, in row 6 either C5R6 or C6R6 must be a 3; therefore, C4R5 cannot be a 3 and then its options are 25. Looking at column 4, the only choice for a 3 is C4R1. Now your grid should look like Example #72.5 below:
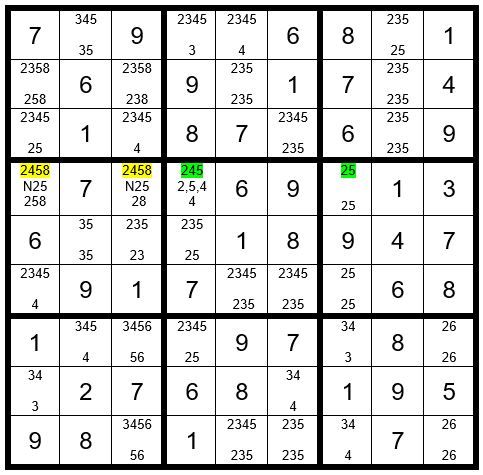
Then, C2R1=5, C1R3=2 and C1R2=8. Now we know that C1R4 cannot be a 2 regardless of which option is correct for C4R4, and the 2 can be eliminated as an option from C1R4. Now your grid should look like Example #72.6 below:
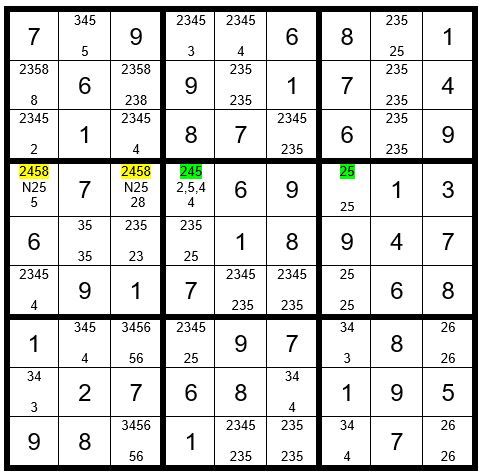
Example #72.6
We will continue the track to see what else we can learn. It so happens that the puzzle tracks out entirely. Please see Example #72.7 below:
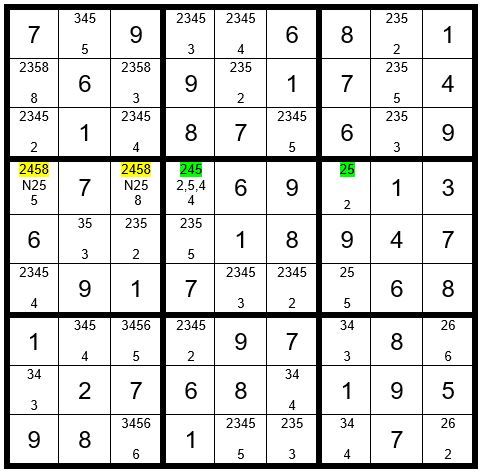
Looking at the puzzle above, what have we learned? The 4 in the driver cell C4R4 tracked out completely without creating a conflict (such as repeating a number in a column, row or cell). Thus, we have solved the problem logically. (Had we created a conflict, then we would have deducted that C4R4 could not be a 4 and it could have been removed as an option for that cell.)
The need to use Step 8 in a Sudoku Puzzle is somewhat rare, but you can see how valuable it was given this very complex puzzle.
May the gentle winds of Sudoku be at your back.
Dan LeKander
Editor's Note: Again, I want to thank Dan…and his proofreader… Peggy!
Each month I copy the article - insert the examples and then shake my head as I realize just how much work goes into each one of the Dan's articles. I have the easy job, his is difficult and then you, our readers, have the challenge. That a team. How many puzzles have you solved?
It was back in January 2016, when we published a final article in Dan's Series of Steps to learn the logic of Sudoku – he asked if we would like a puzzle to solve every month … this editor said an enthusiastic… Yes, please!
If you have not already done so, I suggest you purchase Dan’s book: