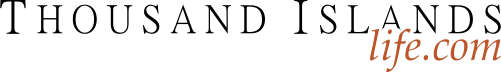Sudoku Puzzle #70
by: Dan LeKander
Great bass fishing on the St. Lawrence River is calling, so this “impossible” puzzle will be short!
Editor's Note: Oh My Goodness... 70 puzzles! Thank you Dan LeKander, not only do we appreciate your wonderful puzzles... but your stopping every month to write these for TI Life goes way beyond a call of duty. Much appreciated....
DAN’S 8-STEP APPROACH TO SOLVING ALL SUDOKU PUZZLES
Once you have completed the puzzle, to the extent that you have filled-in all obvious answers and have written all potential options across the top of the unsolved cells (PUZZLE PREPARATION), Dan recommends the following Steps to complete the puzzle.
Step 1: Sudoku Pairs, Triplets and Quads – See September 2015
Step 2: Turbos & Interaction – See October 2015
Step 3: Sudoku Gordonian Rectangles and Polygons – See November 2015
Step 4: XY-Wings & XYZ Wings – See December 2015
Step 5: X-Wings – See January 2016
Step 6: DAN’S YES/NO CHALLENGE
Step 7: DAN’S CLOSE RELATIONSHIP CHALLENGE
Step 8: AN EXPANSION OF STEP 7Steps 1-5 are relatively common techniques and are explained in the TI LIFE articles above. Steps 6-8 are covered in detail, in Dan’s book.

PUZZLE PREPARATION
Prior to utilizing techniques first complete the 5 Steps of Puzzle Preparation …
- FILL IN DATA FROM OBSERVATIONS, such as obvious pairs or triplets
- FILL IN OBVIOUS ANSWERS
- FILL IN NOT-SO-OBVIOUS ANSWERS
- MARK UNSOLVED CELLS WITH OPTIONS THAT CANNOT EXIST IN THOSE CELLS
- FILL IN THE OPTIONS FOR THE UNSOLVED CELLS
We will complete all of the first 4 steps in the order we observe them.
We will start with the 1’s and navigate through 2’s to 9’s, then repeat the process until we conclude all Puzzle Preparation Step 1-4 clues.
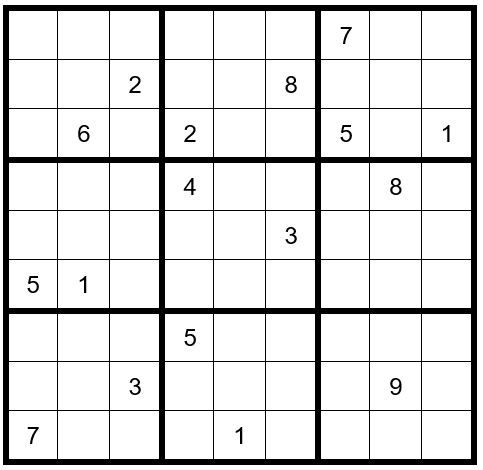
The first thing we observe is that C9R1 (cell in column 9, row 1) =8 (obvious answer). Then, C8R1=2. Now your grid should look like Example #70.1 below:
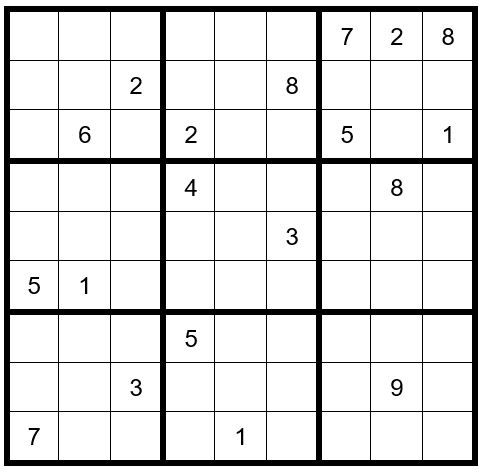
In box 4 a 3 can only exist in C1R4 or C2R4; therefore, a 3 cannot exist as an option in C7R4 or C9R4. Indicate this by placing a small 3 in the bottom of those two cells.
In box 3 a 6 can only exist in C7R2, C8R2 or C9R2; therefore, a 6 cannot exist as an option in C4R2 or C5R2.
In box 3 a 9 can only exist as an option in C7R2 & C9R2; therefore, a 9 cannot exist as an option in any other unsolved cell in row 2.
Additionally, in column 6 the options 15 can only exist in C6R1 or C6R4.
Now your grid should look like Example #70.2 below:
This concludes Puzzle Preparation steps 1-4. We will now fill in the options for the unsolved cells. Now your grid should look like Example #70.3 below:
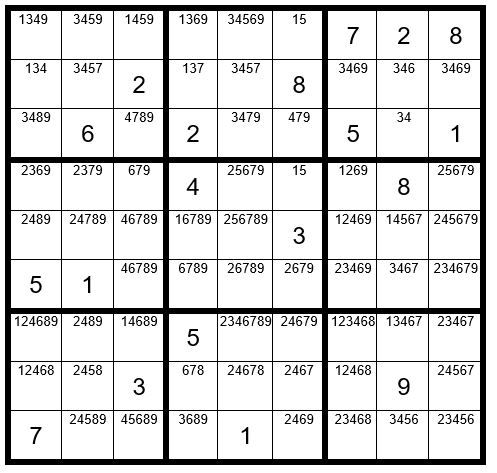
TECHNIQUE STEPS 1-8
There are no Step 1-5 clues. We will now proceed to Step 6: Dan’s Yes-No Challenge.
There are 3 circumstances that establish the potential for a Step 6 exercise:
- Look for just 2 unsolved cells in a box that contain the same option where these 2 cells are not in the same row or column.
- Look for just 2 unsolved cells in a column that contain the same option where these 2 cells are not in the same box.
- Look for just 2 unsolved cells in a row that contain the same option where these 2 cells are not in the same box.
We will start by searching the 1’s to see if there is a potential Step 6 clue, and then navigate through the 2-9’s.
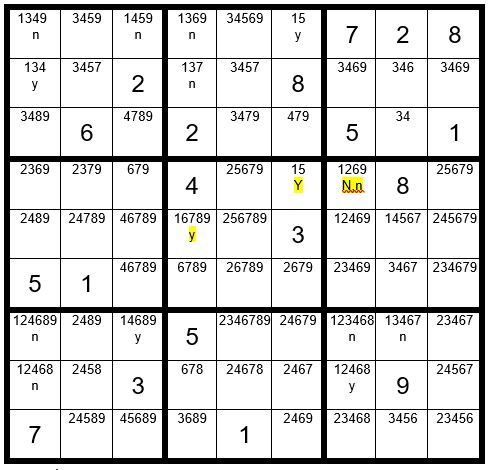
In the example above we find two unsolved cells in box 5 that have the option 1, and are not in the same row or column, thereby qualifying for a Step 6 exercise. We will call these two cells our “driver cells” which drive the exercise. One of these two cells must be a 1. We will first start with C6R4 and assume it is the 1 to see what effect it has on the other unsolved cells with option 1. Then, we will assume C4R5 is the 1, to see what effect it has on the other unsolved cells. We will annotate C6R4 with a “Y” for yes, and annotate C4R5 with “y” to indicate yes.
If C6R4 is the 1, then C7R4 is not a 1, indicated by an N.
If C4R6 is the 1, then C4R1 & C4R2=n. C6R1=y. C1RI & C3R1=n. C1R2=y. C1R7 & C1R8=n. C3R7=y. C7R7 & C8R7=n. C7R8=y. C7R4=n.
You can see that C7R4 has a N,n designation . This means regardless of which of the two driver cells in box 5 is a 1, this cell cannot be a 1. You may eliminate the 1 as an option from this unsolved cell, giving us Example #70.5 below:
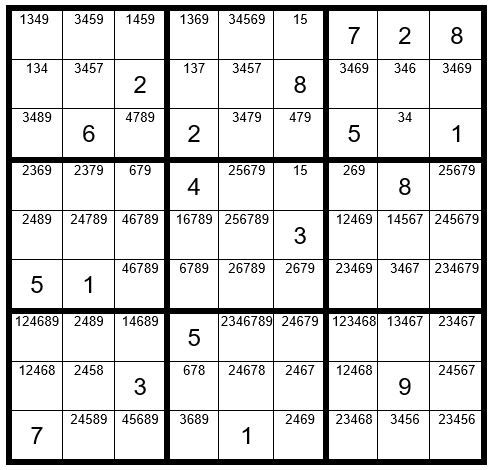
We can see above that the only unsolved cell in row 4 with a 1 as an option is C6R4. C6R4=1. From this point, it is an easy solution, and your completed puzzle should look like Example #70.6 below:
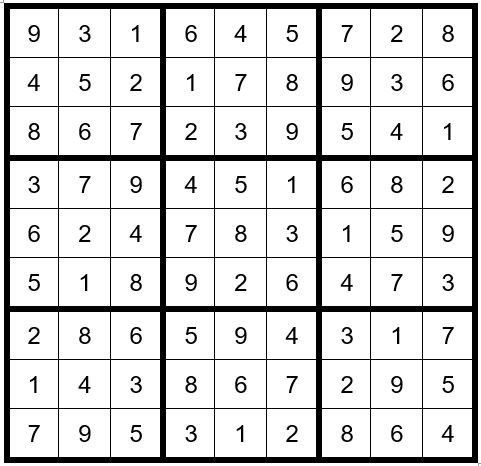
Time to go bass fishing. Please remember the fine principles of catch-and-release.
If you must keep a fish, please keep the fish you plan to eat that day. Next year you will have a good chance of catching the same fish again, only a half to a pound heavier!
May the gentle winds of Sudoku be at your back.
By Dan LeKander
Again, I want to thank Dan…and his proofreader… Peggy! Again... it is amazing that we are posting #70! This editor can find 1001 reasons to do something other than dusting... so I know how hard it is to actually buckle down and not go fishing. So thank you Mr. and Mrs. LeKander - we have come a long from from 2016!
It was back in January 2016, when we published a final article in Dan's Series of Steps to learn the logic of Sudoku – he asked if we would like a puzzle to solve every month … this editor said an enthusiastic… Yes, please!
If you have not already done so, I suggest you purchase Dan’s book: