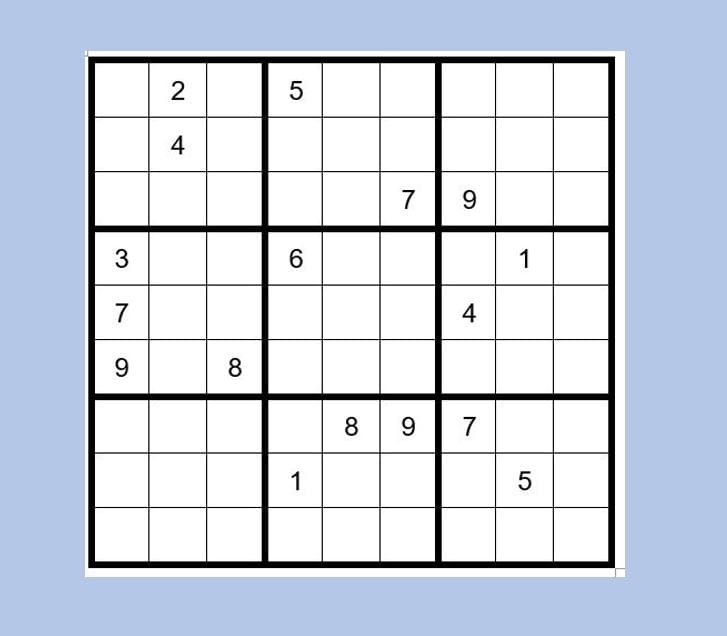
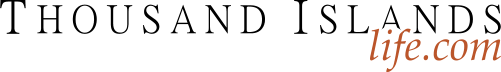Sudoku Puzzle 64
by: Dan LeKander
A few readers requested the “impossible series” continue. Give this one a go and elevate your game to the highest level!
DAN’S 8-STEP APPROACH TO SOLVING ALL SUDOKU PUZZLES
Once you have completed the puzzle, to the extent that you have filled-in all obvious answers and have written all potential options across the top of the unsolved cells (PUZZLE PREPARATION), Dan recommends the following Steps to complete the puzzle.
Step 1: Sudoku Pairs, Triplets and Quads – See September 2015
Step 2: Turbos & Interaction – See October 2015
Step 3: Sudoku Gordonian Rectangles and Polygons – See November 2015
Step 4: XY-Wings & XYZ Wings – See December 2015
Step 5: X-Wings – See January 2016
Step 6: DAN’S YES/NO CHALLENGE
Step 7: DAN’S CLOSE RELATIONSHIP CHALLENGE
Step 8: AN EXPANSION OF STEP 7Steps 1-5 are relatively common techniques and are explained in the TI LIFE articles above. Steps 6-8 are covered in detail, in Dan’s book.

PUZZLE PREPARATION
Prior to utilizing techniques first complete the 5 Steps of Puzzle Preparation …
- FILL IN DATA FROM OBSERVATIONS
- FILL IN OBVIOUS ANSWERS
- FILL IN NOT-SO-OBVIOUS ANSWERS
- MARK UNSOLVED CELLS WITH OPTIONS THAT CANNOT EXIST IN THOSE CELLS
- FILL IN THE OPTIONS FOR THE UNSOLVED CELLS
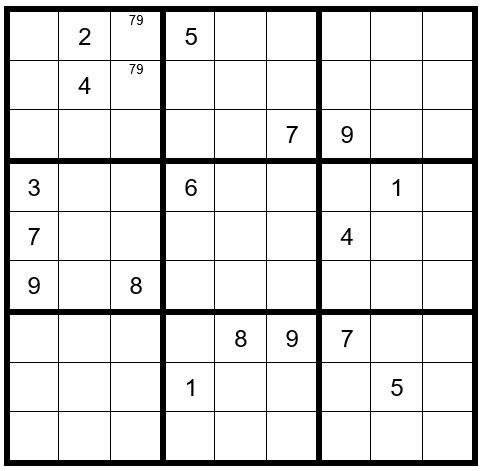
First, we will look for obvious pairs. C3R1 & C3R2 are the only two unsolved cells in box one that can have options 7 & 9, so mark your grid as such, giving you Example #64.1 below:
Now we will complete all of the first 4 steps in the order we observe them, versus all step 1, then step 2, step 3, and step 4 in order, before we move on to step 5.
We will start with the 1’s and navigate through 2’s to 9’s, then repeat the process until we conclude all step 1-4 clues.
The first thing we observe is that C3R4 (cell in column 3, row 4) =4 (obvious answer). Then, C3R5=2.
C2R4/5/6 must have options 156. There is already a 1 & 6 in row 4; therefore, C2R4=5.
C2R3/7/8/9 must have options 3789. There is already a 7,8 & 9 in row 8; therefore, C2R7=3.
C2R3/8/9 must have options 789. There is already a 7 & 9 in row 3; therefore, C2R3=8. Then, C3R3=3.
C1R1/2/3 must have options 156. Enter those on your grid.
C1R6/7/8 must have options 248. Enter those on your grid.
C3R7/8/9 must have options 156. There is already a 1 & 5 in row 8; therefore, C3R8=6.
In box 8 the option 5 can only exist in C5R8 or C5R9; therefore, C3R9 cannot be a 5. We now know that C3R7=5 and C3R9=1.
The only cell in row 7 that can be a 1 is R9R7. C9R7=1.
In box 8 C5R9 & C6R9 must have options 56. Enter those on your grid. Then, in box 9 a 6 can only exist as an option in C8R7. C8R7=6.
Now your grid should look like Example #64.2 below:
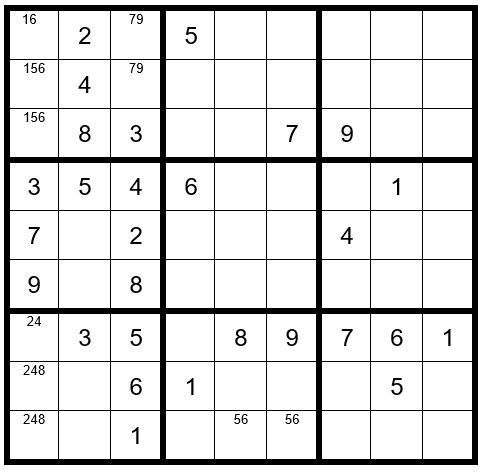
We have now completed Puzzle Preparation steps 1-4, so we will fill in the options for the re-maining unsolved cells.
As we fill in the options, we notice that C6R4 & C7R4 have options 28, an obvious pair. C4R3 & C4R7 have options 24, another obvious pair. C4R6 & C4R9 have options 37, another obvious pair, C4R3 & C8R3 have options 24, yet another obvious pair. Take these obvious pairs into account when filling in the remaining options.
Now your grid should look like Example #64.3 below:
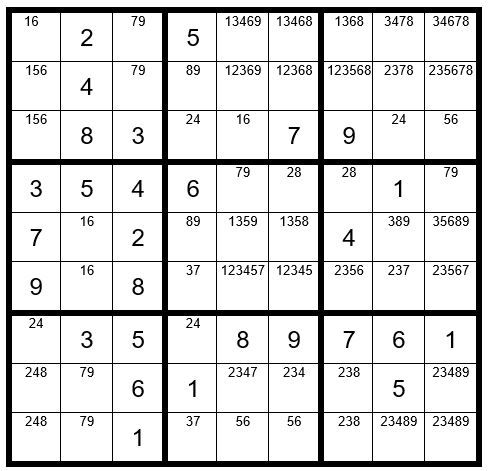
Steps 1-5
The first thing we notice is in column 7. C7R4/8/9 form an obvious triplet, and therefore, no other unsolved cell in column 7 may have a 2, 3 or 8 as an option.
C7R1, C7R2 & C9R3 now form an obvious triplet, therefore, no other unsolved cell in box 3 may have a 1, 5 or 6 as an option.
We now have an obvious pair in row 1, therefore, no other unsolved cell in row 1 may have 1 or 6 as an option.
In box 3 we find a triplet 156; therefore, remove the options 5 and 6 from C9R2.
Lastly, in column 7 the only unsolved cells that have a 3 as an option are C7R8 & C7R9. Therefore, no other unsolved cell in box 9 may have a 3 as an option. This is an example of an Interaction.
Now your grid should look like Example #64.4 below:
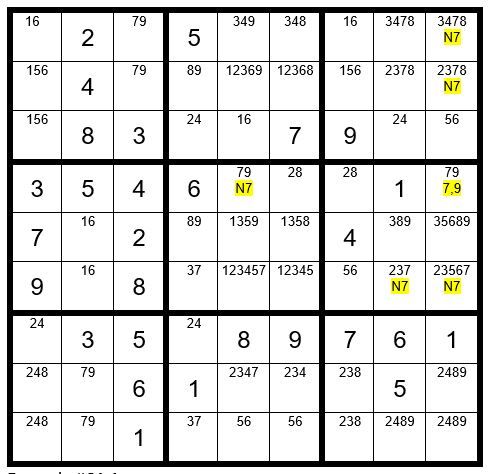
We will now proceed to Step 6: Dan’s Yes-No Challenge. We will start by searching the 1’s to see if there is a potential Step 6 clue, and then navigate through the 2-9’s. We find no Step 6 viable clues.
We will move on to Step 7:
Dan’s Close Relationship Challenge. In this exercise we will select any two-option unsolved cell as the driver cell. My first choice is C9R4, with the sequence 7,9 as marked above. I chose this cell and sequence because this cell has 5 adjacent unsolved cells with 7 as an option and the 9 may track through the puzzle to give us significant information.
We know that C9R4 must be a 7 or 9. First, we will assume it is a 7. If this is true, then C9R1, C9R2, C5R4, C8R6 & C9R6 cannot be a 7 (hence the notation N7).
Next, we will assume C9R4 is a 9. If this is true, then not all of the N7 cells can be a 7. This exercise is to determine which of those 5 cells cannot be a 7.
The next step is to “track” the influence of C9R4 being a 9 through the puzzle to see what the value would be for the N7 cells, with the theory being if a N7 cell is a value other than a 9, then it is not a 7 regardless if the driver cell is a 7 or 9, and the 7 can be eliminated as an option for that cell. We will track the 9 through the puzzle in Example #64.5 below:
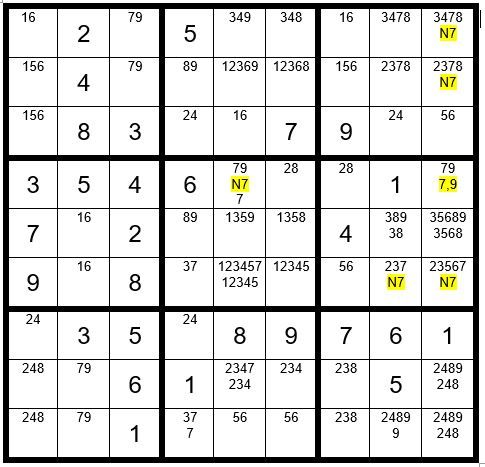
We see that if C9R4=9, then C8R9=9,C5R4=7, and C4R9=7. You can see that we already have a 7 and 9 in row 9, leaving C2R9 without no choice for a solution.
This is a conflict; therefore, we have quickly learned that C9R4 cannot be a 9, and thus, C9R4=7. It follows that C5R4=9. C4R5=8. C4R2=9. C6R4=2. C7R4=8. C3R2=7. C3R1=9. C8R1=7. Now your grid should look like Example #64.6 below:
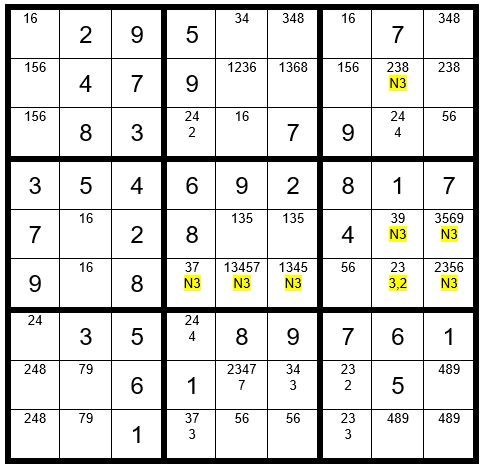
Looks like we will need to perform another Step 7 for further clues. We’ll choose C8R6 with sequence 3,2 as per above example. Next, we will track the option 2 starting in C8R6, with the results per example above. Oops, we have 2 3’s in row 9, leading us to the conclusion that C8R6 cannot be a 2; therefore, C8R6=3. It then follows that C8R5=9. C4R6=7. C4R9=3. C7R9=2. C7R8=3. C6R8=4. C4R7=2. C4R3=4. C8R3=2. C8R2=8. C8R9=4. C1R9=8. C9R9=9. C9R8=8. C2R9=7. C2R8=9. C1R7=4. C1R8=2. C5R8=7. C5R6=4. C5R1=3. C6R1=8. C9R1=4. C5R2=2. C9R2=3. C6R5=3. C9R6=2. Now your grid should look like Example #64.7 below:
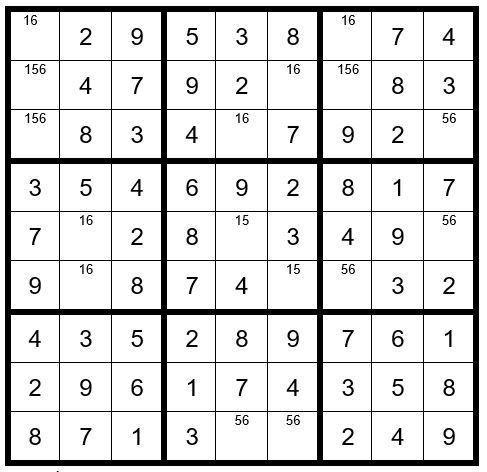
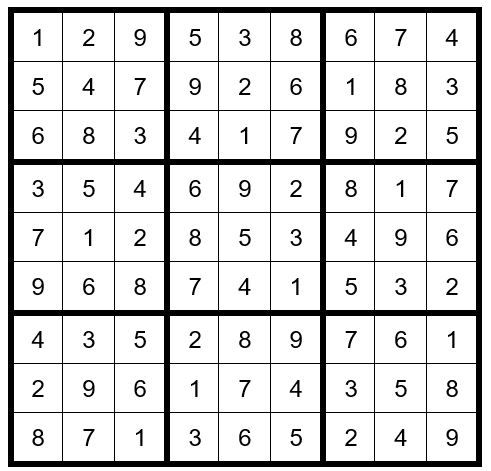
Performing another Step 7 with C6R2 and sequence 6,1 you will quickly learn that C6R2 cannot be a 1; therefore, C6R2=6, leading to an easy conclusion as per Example #64.8 below:
If you will please e-mail me at djlsuniverse@yahoo.com with any questions, comments, or suggestions, I would enjoy hearing from you. It would be of benefit to know your age and your skill level.
May the gentle winds of Sudoku be at your back.
May the gentle winds of Sudoku be at your back.
By Dan LeKander
Editor's Note:
Each month I write that it was back in January 2016, when we published a final article in Dan's Series of Steps to learn the logic of Sudoku – that he asked if we would like a puzzle to solve every month … this editor said an enthusiastic… Yes, please! Now we are several years later and on Puzzle #64.
If you have not already done so, I suggest you purchase Dan’s book: